| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 7 Triangles
Welcome to this comprehensive resource offering meticulously detailed solutions for the NCERT Exemplar problems designed for Class 9 Mathematics, Chapter 7: Triangles. These Exemplar questions represent a significant leap in complexity compared to standard textbook exercises, deliberately focusing on strengthening deductive reasoning skills through challenging proofs and applications involving Congruence of Triangles and Triangle Inequalities. The emphasis shifts firmly from calculation to rigorous logical argumentation, demanding a deep and precise understanding of geometric principles.
A cornerstone of this chapter is the concept of Congruence. Our solutions provide exhaustive guidance on understanding and applying the four fundamental criteria for proving triangles congruent:
- SSS (Side-Side-Side): If three sides of one triangle are equal to the three corresponding sides of another.
- SAS (Side-Angle-Side): If two sides and the included angle of one triangle are equal to the corresponding parts of another.
- ASA (Angle-Side-Angle): If two angles and the included side of one triangle are equal to the corresponding parts of another.
- RHS (Right angle-Hypotenuse-Side): If the hypotenuse and one side of a right-angled triangle are equal to the corresponding parts of another right-angled triangle.
The solutions demonstrate not just how to apply these criteria ($\cong$), but also the crucial preliminary steps of correctly identifying corresponding vertices, sides, and angles. A vital tool employed extensively is CPCTC (Corresponding Parts of Congruent Triangles are Congruent), used to deduce the equality of other sides or angles once congruence has been established. Exemplar problems often feature complex diagrams where identifying the correct triangles to compare, or proving intermediate congruences first, is non-trivial. Properties derived from congruence, especially those concerning isosceles triangles (angles opposite equal sides are equal, and its converse theorem: sides opposite equal angles are equal), are frequently leveraged in subsequent proofs or related problems.
The second major pillar explored in depth is Triangle Inequalities. These theorems govern the relationships between the sides and angles within a single triangle. The solutions clearly explain and demonstrate the application of key inequality principles:
- The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
- In any triangle, the angle opposite the longer side is larger than the angle opposite the shorter side.
- Conversely, in any triangle, the side opposite the larger angle is longer than the side opposite the smaller angle.
Exemplar problems often require applying these inequalities strategically to prove relationships between sides and angles, establish possible ranges for side lengths, or prove geometric inequalities within complex figures. Solving these sometimes necessitates clever auxiliary constructions or the combined application of inequalities with other results like the exterior angle theorem.
Addressing diverse question formats (MCQs testing criteria/properties, Fill-in-the-Blanks, True/False probing subtle conditions, and Short/Long Answer questions demanding rigorous proofs), these solutions offer clear diagrams, meticulously structured step-by-step logical proofs with explicit justifications for each step (citing relevant theorems, postulates, or congruence criteria), and effective strategies for navigating complex geometric arguments. This resource is invaluable for any student aiming to master the art of geometric proof related to triangles, building a solid foundation for more advanced geometry.
Sample Question 1 (Before Exercise 7.1)
Write the correct answer:
Sample Question 1: If ∆ ABC ≅ ∆ PQR and ∆ ABC is not congruent to ∆ RPQ, then which of the following is not true:
(A) BC = PQ
(B) AC = PR
(C) QR = BC
(D) AB = PQ
Answer:
Given Information:
We are given two conditions regarding two triangles, $\triangle ABC$ and $\triangle PQR$:
$\triangle ABC \cong \triangle PQR$
... (i)
and
$\triangle ABC$ is not congruent to $\triangle RPQ$
... (ii)
Analysis and Solution:
The first and primary condition given is that $\triangle ABC \cong \triangle PQR$.
When two triangles are congruent, their corresponding parts are equal. This is known as CPCTC (Corresponding Parts of Congruent Triangles are Equal). The order of the vertices in the congruence statement tells us which parts correspond.
The correspondence is: A ↔ P, B ↔ Q, and C ↔ R.
Based on this correspondence, we can state the following equalities between the sides:
1. AB = PQ
2. BC = QR
3. AC = PR
Now, let's evaluate the given options against these true statements:
(B) AC = PR: This statement is true, as it is a direct result of the given congruence.
(C) QR = BC: This statement is also true, as it is the same as BC = QR, which is a direct result of the congruence.
(D) AB = PQ: This statement is true, as it is a direct result of the congruence.
(A) BC = PQ: This statement is not a direct consequence of the congruence $\triangle ABC \cong \triangle PQR$. From the congruence, we know that $BC = QR$ and $AB = PQ$. Therefore, the statement $BC = PQ$ would only be true if $QR = PQ$. This is a special condition where the triangle $\triangle PQR$ would be isosceles. Since this is not true for all triangles, the statement $BC = PQ$ is not necessarily true.
Since the question asks which of the following is "not true", and we have established that options (B), (C), and (D) are always true based on the given congruence, the statement that is not necessarily true is (A).
(The second condition, that $\triangle ABC$ is not congruent to $\triangle RPQ$, is extra information that prevents the triangles from being equilateral, but it doesn't change our conclusion).
Therefore, the correct option is (A).
Exercise 7.1
In each of the following, write the correct answer:
Question 1. Which of the following is not a criterion for congruence of triangles?
(A) SAS
(B) ASA
(C) SSA
(D) SSS
Answer:
There are several well-established criteria for proving the congruence of two triangles. These criteria ensure that if certain corresponding sides and/or angles are equal, then the triangles are identical in shape and size.
The common congruence criteria are:
- SSS (Side-Side-Side): If three sides of one triangle are respectively equal to the three sides of another triangle, then the two triangles are congruent.
- SAS (Side-Angle-Side): If two sides and the included angle of one triangle are respectively equal to two sides and the included angle of another triangle, then the two triangles are congruent.
- ASA (Angle-Side-Angle): If two angles and the included side of one triangle are respectively equal to two angles and the included side of another triangle, then the two triangles are congruent.
- AAS (Angle-Angle-Side): If two angles and a non-included side of one triangle are respectively equal to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent. (Note: AAS is equivalent to ASA because if two angles are known, the third angle is also determined by the angle sum property of a triangle).
- RHS (Right angle-Hypotenuse-Side): If in two right-angled triangles, the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Looking at the given options:
- (A) SAS is a valid congruence criterion.
- (B) ASA is a valid congruence criterion.
- (C) SSA (Side-Side-Angle) is generally not a criterion for congruence. This is because knowing two sides and a non-included angle can sometimes lead to two different possible triangles (the ambiguous case of the Sine Rule).
- (D) SSS is a valid congruence criterion.
Therefore, the option that is not a criterion for congruence of triangles is SSA.
The correct answer is (C) SSA.
Question 2. If AB = QR, BC = PR and CA = PQ, then
(A) ∆ ABC ≅ ∆ PQR
(B) ∆ CBA ≅ ∆ PRQ
(C) ∆ BAC ≅ ∆ RPQ
(D) ∆ PQR ≅ ∆ BCA
Answer:
Given:
We are given two triangles, $\triangle ABC$ and $\triangle PQR$, with the following side equalities:
AB = QR
BC = PR
CA = PQ
Analysis and Solution:
Since all three sides of one triangle are equal to the corresponding three sides of the other triangle, the two triangles are congruent by the SSS (Side-Side-Side) congruence rule.
To write the correct congruence statement, we must match the corresponding vertices. We can do this by looking at which vertices are the endpoints of the equal sides.
- Side AB = Side QR
- Side BC = Side PR
- Side CA = Side PQ
Let's find the vertex correspondence:
- Vertex A is the common point of sides AB and CA. The corresponding sides are QR and PQ. Their common point is vertex Q. Thus, A ↔ Q.
- Vertex B is the common point of sides AB and BC. The corresponding sides are QR and PR. Their common point is vertex R. Thus, B ↔ R.
- Vertex C is the common point of sides BC and CA. The corresponding sides are PR and PQ. Their common point is vertex P. Thus, C ↔ P.
So, the correct correspondence of vertices is: A ↔ Q, B ↔ R, and C ↔ P.
Now let's check the given options against this correct correspondence:
(A) ∆ ABC ≅ ∆ PQR: This implies A ↔ P, B ↔ Q, C ↔ R. This is incorrect.
(B) ∆ CBA ≅ ∆ PRQ: This implies C ↔ P, B ↔ R, A ↔ Q. This matches our derived correspondence. This is correct.
(C) ∆ BAC ≅ ∆ RPQ: This implies B ↔ R, A ↔ P, C ↔ Q. This is incorrect.
(D) ∆ PQR ≅ ∆ BCA: This implies P ↔ B, Q ↔ C, R ↔ A. This is incorrect.
The only statement that correctly represents the congruence based on the given side equalities is option (B).
Hence, the correct option is (B) ∆ CBA ≅ ∆ PRQ.
Question 3. In ∆ ABC, AB = AC and ∠B = 50°. Then ∠C is equal to
(A) 40°
(B) 50°
(C) 80°
(D) 130°
Answer:
In any triangle, if two sides are equal, then the angles opposite to these sides are also equal. This property is characteristic of an isosceles triangle.
Given that in $\triangle ABC$, we have $AB = AC$.
The side $AB$ is opposite to angle $\angle C$.
The side $AC$ is opposite to angle $\angle B$.
Since $AB = AC$, the angles opposite to these sides must be equal.
Therefore, $\angle B = \angle C$.
We are given that $\angle B = 50^\circ$.
Using the property $\angle B = \angle C$, we can conclude that $\angle C$ is also equal to $50^\circ$.
$\angle C = \angle B$
$\angle C = 50^\circ$
(Since $\angle B = 50^\circ$)
The options are:
- (A) $40^\circ$
- (B) $50^\circ$
- (C) $80^\circ$
- (D) $130^\circ$
Our calculated value for $\angle C$ is $50^\circ$, which matches option (B).
The correct answer is (B) $50^\circ$.
Question 4. In ∆ ABC, BC = AB and ∠B = 80°. Then ∠A is equal to
(A) 80°
(B) 40°
(C) 50°
(D) 100°
Answer:
Given: In $\triangle ABC$, $BC = AB$ and $\angle B = 80^\circ$.
To Find: The measure of $\angle A$.
Solution:
In $\triangle ABC$, we are given that $BC = AB$.
According to the property of isosceles triangles, the angles opposite to equal sides are equal.
The angle opposite to side $BC$ is $\angle A$.
The angle opposite to side $AB$ is $\angle C$.
Since $BC = AB$, the angles opposite to these sides must be equal.
$\angle A = \angle C$
The sum of the interior angles in any triangle is $180^\circ$.
In $\triangle ABC$, the angle sum property states:
$\angle A + \angle B + \angle C = 180^\circ$
... (i)
Substitute the given value $\angle B = 80^\circ$ and the relation $\angle C = \angle A$ into equation (i):
$\angle A + 80^\circ + \angle A = 180^\circ$
Combine the terms involving $\angle A$:
$2\angle A + 80^\circ = 180^\circ$
Subtract $80^\circ$ from both sides of the equation:
$2\angle A = 180^\circ - 80^\circ$
$2\angle A = 100^\circ$
Divide both sides by 2 to find the value of $\angle A$:
$\angle A = \frac{100^\circ}{2}$
$\angle A = 50^\circ$
Comparing this result with the given options:
- (A) $80^\circ$
- (B) $40^\circ$
- (C) $50^\circ$
- (D) $100^\circ$
The calculated value of $\angle A$ is $50^\circ$, which matches option (C).
The correct answer is (C) $50^\circ$.
Question 5. In ∆ PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is
(A) 4 cm
(B) 5 cm
(C) 2 cm
(D) 2.5 cm
Answer:
Given:
In $\triangle PQR$, $\angle R = \angle P$, $QR = 4$ cm, and $PR = 5$ cm.
To Find:
The length of side PQ.
Solution:
In a triangle, the sides opposite to equal angles are equal in length.
We are given that in $\triangle PQR$, $\angle R = \angle P$.
The side opposite to $\angle R$ is $PQ$.
The side opposite to $\angle P$ is $QR$.
Since $\angle R = \angle P$, the sides opposite these angles must be equal.
PQ = QR
We are given that $QR = 4$ cm.
Substituting this value into the equation $PQ = QR$:
PQ = 4 cm
The length of side PQ is 4 cm.
Comparing this result with the given options:
- (A) 4 cm
- (B) 5 cm
- (C) 2 cm
- (D) 2.5 cm
The calculated value of PQ matches option (A).
The correct answer is (A) 4 cm.
Question 6. D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then
(A) BD = CD
(B) BA > BD
(C) BD > BA
(D) CD > CA
Answer:
Given:
In a triangle $\triangle ABC$, D is a point on the side BC.
The line segment AD is the bisector of the angle $\angle BAC$.
To Find:
Which of the given relationships is always true.
Analysis and Solution:
The core principle we will use is the relationship between angles and their opposite sides in a triangle: In a triangle, the side opposite the larger angle is longer.
Let's analyze the options by examining the smaller triangles formed by the angle bisector AD, which are $\triangle ABD$ and $\triangle ACD$.
Consider the triangle $\triangle ACD$.
The angle $\angle BDA$ is an exterior angle to $\triangle ACD$.
By the Exterior Angle Theorem, an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
$\angle BDA = \angle CAD + \angle ACD$
[Exterior Angle Theorem]
Note that $\angle ACD$ is the same as $\angle C$.
$\angle BDA = \angle CAD + \angle C$
... (i)
We are given that AD bisects $\angle BAC$. This means it divides the angle into two equal parts:
$\angle BAD = \angle CAD$
[AD is the angle bisector]
Now, substitute $\angle BAD$ in place of $\angle CAD$ in equation (i):
$\angle BDA = \angle BAD + \angle C$
Since $\angle C$ is an angle of a triangle, its measure must be positive ($\angle C > 0^\circ$).
From the equation above, it is clear that $\angle BDA$ is greater than $\angle BAD$.
$\angle BDA > \angle BAD$
Now let's apply the side-angle relationship to the triangle $\triangle ABD$.
- The side opposite to $\angle BDA$ is BA.
- The side opposite to $\angle BAD$ is BD.
Since $\angle BDA > \angle BAD$, the side opposite $\angle BDA$ must be longer than the side opposite $\angle BAD$.
Therefore, we can conclude that:
BA > BD
This matches option (B).
Why other options are incorrect:
- (A) BD = CD: This is only true if AD is a median, which happens when the triangle is isosceles ($\triangle ABC$ with AB = AC). It is not always true.
- (C) BD > BA: This would imply $\angle BAD > \angle BDA$, which we have just proved to be false.
- (D) CD > CA: In $\triangle ACD$, this would imply $\angle CAD > \angle CDA$. Since $\angle CDA = \angle BDA$, this is the same as $\angle CAD > \angle BDA$. We know from equation (i) that $\angle BDA = \angle CAD + \angle C$, so $\angle BDA > \angle CAD$. Thus, this option is false. The correct relationship is CA > CD.
Hence, the correct option is (B) BA > BD.
Question 7. It is given that ∆ABC ≅∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
(A) DF = 5 cm, ∠F = 60°
(B) DF = 5 cm, ∠E = 60°
(C) DE = 5 cm, ∠E = 60°
(D) DE = 5 cm, ∠D = 40°
Answer:
Given:
We are given that two triangles are congruent:
$\triangle ABC \cong \triangle FDE$
And we have the following measurements for $\triangle ABC$:
- AB = 5 cm
- $\angle B = 40^\circ$
- $\angle A = 80^\circ$
To Find:
Which of the given options is true.
Analysis and Solution:
First, let's find the third angle of $\triangle ABC$ using the angle sum property of a triangle (sum of angles is $180^\circ$).
$\angle A + \angle B + \angle C = 180^\circ$
$80^\circ + 40^\circ + \angle C = 180^\circ$
$120^\circ + \angle C = 180^\circ$
$\angle C = 180^\circ - 120^\circ$
$\angle C = 60^\circ$
Now, we use the given congruence statement, $\triangle ABC \cong \triangle FDE$. This tells us which parts of the triangles correspond and are therefore equal (CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
The correspondence is as follows:
Vertices: A ↔ F, B ↔ D, C ↔ E
Using this correspondence, we can find the properties of $\triangle FDE$:
Corresponding Sides:
- AB = FD (or DF). Since AB = 5 cm, then DF = 5 cm.
- BC = DE
- AC = FE
Corresponding Angles:
- $\angle A = \angle F$. Since $\angle A = 80^\circ$, then $\angle F = 80^\circ$.
- $\angle B = \angle D$. Since $\angle B = 40^\circ$, then $\angle D = 40^\circ$.
- $\angle C = \angle E$. Since $\angle C = 60^\circ$, then $\angle E = 60^\circ$.
Now we can check the given options:
(A) DF = 5 cm, ∠F = 60°: The first part is true (DF = 5 cm), but the second part is false ($\angle F$ is $80^\circ$, not $60^\circ$). So, this option is incorrect.
(B) DF = 5 cm, ∠E = 60°: The first part is true (DF = 5 cm) and the second part is also true ($\angle E = 60^\circ$). So, this option is true.
(C) DE = 5 cm, ∠E = 60°: The first part is false (DE corresponds to BC, not AB, so we don't know its length). The second part is true ($\angle E = 60^\circ$). Since one part is false, this option is incorrect.
(D) DE = 5 cm, ∠D = 40°: The first part is false. The second part is true ($\angle D = 40^\circ$). Since one part is false, this option is incorrect.
The only option where both statements are true is (B).
Hence, the correct option is (B) DF = 5 cm, ∠E = 60°.
Question 8. Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
(A) 3.6 cm
(B) 4.1 cm
(C) 3.8 cm
(D) 3.4 cm
Answer:
Given:
Two sides of a triangle have lengths 5 cm and 1.5 cm.
To Determine:
The length that the third side of the triangle cannot be from the given options.
Solution:
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Also, the difference between the lengths of any two sides must be less than the length of the third side.
Let the length of the third side be $x$ cm.
Applying the Triangle Inequality Theorem:
1. The sum of the two given sides must be greater than the third side:
$5 + 1.5 > x$
$6.5 > x$
or $x < 6.5$
2. The sum of the third side and one of the given sides must be greater than the other given side:
$x + 5 > 1.5$
This inequality is always true since $x$ must be a positive value (length of a side) and $5 > 1.5$.
$x + 1.5 > 5$
$x > 5 - 1.5$
$x > 3.5$
Combining the inequalities $x < 6.5$ and $x > 3.5$, we find that the length of the third side $x$ must satisfy the condition $3.5 < x < 6.5$.
Now let's check the given options to see which one does not fall within this range:
- (A) 3.6 cm: $3.5 < 3.6 < 6.5$. This is a possible length.
- (B) 4.1 cm: $3.5 < 4.1 < 6.5$. This is a possible length.
- (C) 3.8 cm: $3.5 < 3.8 < 6.5$. This is a possible length.
- (D) 3.4 cm: Is $3.5 < 3.4$? No. $3.4$ is not greater than $3.5$. This length does not satisfy the triangle inequality.
Therefore, the length of the third side of the triangle cannot be 3.4 cm.
The correct answer is (D) 3.4 cm.
Question 9. In ∆ PQR, if ∠R > ∠Q, then
(A) QR > PR
(B) PQ > PR
(C) PQ < PR
(D) QR < PR
Answer:
Given:
In $\triangle PQR$, $\angle R > \angle Q$.
To Determine:
Which of the given statements is true.
Solution:
In any triangle, there is a relationship between the lengths of sides and the measures of their opposite angles. Specifically, the side opposite a larger angle is longer than the side opposite a smaller angle.
We are given that in $\triangle PQR$, the measure of angle R is greater than the measure of angle Q, i.e., $\angle R > \angle Q$.
Let's identify the sides opposite to these angles:
- The side opposite to $\angle R$ is the side PQ.
- The side opposite to $\angle Q$ is the side PR.
Applying the property that the side opposite a larger angle is longer than the side opposite a smaller angle:
Since $\angle R > \angle Q$, the side opposite $\angle R$ must be longer than the side opposite $\angle Q$.
PQ > PR
Now let's examine the given options:
- (A) QR > PR: This compares the side opposite $\angle P$ (QR) with the side opposite $\angle Q$ (PR). This does not directly follow from the given $\angle R > \angle Q$.
- (B) PQ > PR: This compares the side opposite $\angle R$ (PQ) with the side opposite $\angle Q$ (PR). This matches our derived inequality $PQ > PR$.
- (C) PQ < PR: This is the opposite of our derived inequality $PQ > PR$.
- (D) QR < PR: This compares the side opposite $\angle P$ (QR) with the side opposite $\angle Q$ (PR). This does not directly follow from the given $\angle R > \angle Q$.
The statement that is true is PQ > PR.
The correct answer is (B) PQ > PR.
Question 10. In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are
(A) isosceles but not congruent
(B) isosceles and congruent
(C) congruent but not isosceles
(D) neither congruent nor isosceles
Answer:
Given:
We are considering two triangles, $\triangle ABC$ and $\triangle PQR$, with the following properties:
1. In $\triangle ABC$, AB = AC.
2. $\angle C = \angle P$.
3. $\angle B = \angle Q$.
Analysis and Solution:
Let's analyze each triangle based on the given information.
Step 1: Analyze $\triangle ABC$
We are given that in $\triangle ABC$, two sides are equal: AB = AC.
A fundamental property of triangles states that if two sides of a triangle are equal, then the angles opposite to these sides are also equal.
- The angle opposite to side AC is $\angle B$.
- The angle opposite to side AB is $\angle C$.
Therefore, we can conclude that $\angle B = \angle C$.
Since $\triangle ABC$ has two equal sides and two equal angles, it is an isosceles triangle.
Step 2: Analyze $\triangle PQR$
We are given two relationships connecting the angles of the two triangles:
$\angle C = \angle P$
$\angle B = \angle Q$
From Step 1, we established that $\angle B = \angle C$. Combining these three equations, we get:
$\angle P = \angle C = \angle B = \angle Q$
This implies that in $\triangle PQR$, we have $\angle P = \angle Q$.
The converse of the property used in Step 1 states that if two angles of a triangle are equal, then the sides opposite to these angles are also equal.
- The side opposite to $\angle Q$ is PR.
- The side opposite to $\angle P$ is QR.
Therefore, we can conclude that PR = QR.
Since $\triangle PQR$ has two equal sides and two equal angles, it is also an isosceles triangle.
Step 3: Check for Congruence
So far, we have established that both triangles are isosceles. This eliminates options (C) and (D).
Now we need to determine if they are congruent.
For two triangles to be congruent, we need to satisfy one of the congruence rules (like SSS, SAS, ASA, AAS). We know the following about the angles:
$\angle B = \angle Q$
$\angle C = \angle P$
By the angle sum property, the third angles must also be equal: $\angle A = \angle R$.
This means the triangles are similar ($\triangle ABC \sim \triangle RQP$). However, similarity does not guarantee congruence. To be congruent, we need at least one pair of corresponding sides to be equal.
The problem gives us no information linking the side lengths of $\triangle ABC$ to the side lengths of $\triangle PQR$. For example, we do not know if AB = RQ or BC = QP.
Consider an example: Let $\triangle ABC$ have sides AB = AC = 10 cm and angles $\angle B = \angle C = 70^\circ$. Let $\triangle PQR$ have angles $\angle Q = \angle P = 70^\circ$ but with sides PR = QR = 12 cm. Both triangles satisfy all the given conditions, they are both isosceles, but they are clearly not congruent.
Since we cannot prove that the triangles must be congruent, we describe them as "not congruent" (meaning "not necessarily congruent").
Conclusion:
Both triangles are isosceles, but they are not necessarily congruent.
Hence, the correct option is (A) isosceles but not congruent.
Question 11. In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if
(A) BC = EF
(B) AC = DE
(C) AC = EF
(D) BC = DE
Answer:
Given:
We are considering two triangles, $\triangle ABC$ and $\triangle DEF$.
We are given two equalities:
1. AB = FD (A pair of equal sides)
2. $\angle A = \angle D$ (A pair of equal angles)
To Find:
The additional condition required to prove that the two triangles are congruent by the SAS (Side-Angle-Side) axiom.
Analysis and Solution:
The SAS congruence axiom states that two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle.
The "included angle" is the angle that is formed between the two sides.
Let's analyze the parts for each triangle based on the SAS requirement:
In $\triangle ABC$:
- We are using the given side AB.
- We are using the given angle $\angle A$.
- For $\angle A$ to be the included angle, the two sides must be AB and AC. Therefore, the second side we must use is AC.
So, for $\triangle ABC$, the three parts for SAS congruence are: Side AB, Angle A, Side AC.
In $\triangle DEF$:
- The side corresponding to AB is given as FD.
- The angle corresponding to $\angle A$ is given as $\angle D$.
- For $\angle D$ to be the included angle in $\triangle DEF$, the two sides must be FD and DE. Therefore, the second side we must use is DE.
So, for $\triangle DEF$, the corresponding three parts for SAS congruence are: Side FD, Angle D, Side DE.
Now, let's establish the full congruence condition:
For the triangles to be congruent by SAS, all three corresponding parts must be equal.
- Side: AB = FD (Given)
- Angle: $\angle A = \angle D$ (Given)
- Side: AC = DE (This is the required third condition)
Therefore, the condition that must be true for the triangles to be congruent by SAS is AC = DE.
Let's check the given options:
(A) BC = EF
(B) AC = DE
(C) AC = EF
(D) BC = DE
Our derived condition matches option (B).
Hence, the correct option is (B) AC = DE.
Sample Question 1 & 2 (Before Exercise 7.2)
Sample Question 1: In the two triangles ABC and DEF, AB = DE and AC = EF. Name two angles from the two triangles that must be equal so that the two triangles are congruent. Give reason for your answer.
Answer:
Given:
We are given two triangles, $\triangle ABC$ and $\triangle DEF$.
Two pairs of corresponding sides are equal:
AB = DE
AC = EF
To Find:
A pair of angles (one from each triangle) that must be equal for the two triangles to be congruent, and the reason for this.
Solution:
We are given two pairs of equal sides. To prove congruence using this information, the most direct method is the SAS (Side-Angle-Side) congruence criterion.
The SAS criterion states that two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle.
The "included angle" is the angle formed between the two sides.
For $\triangle ABC$:
The given sides are AB and AC.
The angle included between sides AB and AC is $\angle BAC$ (or simply $\angle A$).
For $\triangle DEF$:
The corresponding sides are DE (which equals AB) and EF (which equals AC).
The angle included between sides DE and EF is $\angle DEF$ (or simply $\angle E$).
Therefore, for the triangles to be congruent by the SAS axiom, the included angles must be equal.
Conclusion:
The two angles that must be equal are:
$\angle BAC = \angle DEF$
Reason:
If $\angle BAC = \angle DEF$, then $\triangle ABC$ will be congruent to $\triangle DEF$ by the SAS (Side-Angle-Side) congruence rule, as we would have:
- AB = DE (Given Side)
- $\angle BAC = \angle DEF$ (Included Angle)
- AC = EF (Given Side)
This would establish the congruence: $\triangle ABC \cong \triangle DEF$.
Sample Question 2: In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.
Answer:
Given:
We are given two triangles, $\triangle ABC$ and $\triangle DEF$.
The following conditions are met:
$\angle A = \angle D$
$\angle B = \angle E$
AB = EF
Question:
Will the two triangles be congruent?
Answer and Reasons:
The two triangles will not necessarily be congruent.
Here is the reasoning:
For two triangles to be congruent, a specific congruence rule (like ASA, AAS, SAS, or SSS) must be satisfied. These rules require that the equal parts of one triangle correspond to the equal parts of the other triangle.
Let's establish the correct correspondence based on the given equal angles:
$\angle A = \angle D$
(Given)
$\angle B = \angle E$
(Given)
By the angle sum property of a triangle, if two angles are equal, the third angle must also be equal. Therefore:
$\angle C = \angle F$
This means the correspondence between the vertices is:
A ↔ D, B ↔ E, and C ↔ F.
For the triangles to be congruent (e.g., by the ASA or AAS rule), the equal sides must also correspond. Based on the vertex correspondence above, the corresponding sides are:
- Side AB corresponds to side DE.
- Side BC corresponds to side EF.
- Side AC corresponds to side DF.
To satisfy a congruence criterion like ASA or AAS, we would need the equality of corresponding sides. For example:
- For ASA congruence, we would need $\angle A = \angle D$, AB = DE, and $\angle B = \angle E$.
- For AAS congruence, we could need $\angle A = \angle D$, $\angle B = \angle E$, and BC = EF.
However, the problem states that AB = EF.
In this given equality, the side AB from the first triangle is being equated to the side EF from the second triangle. But according to our correspondence, the side AB corresponds to DE, and the side EF corresponds to BC.
Since the given equal side (AB) is not equal to its corresponding side (DE), but rather to a non-corresponding side (EF), the conditions for congruence are not met.
Therefore, the triangles are not necessarily congruent.
Exercise 7.2
Question 1. In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆ PQR should be equal to side AB of ∆ ABC so that the two triangles are congruent? Give reason for your answer.
Answer:
Given:
In triangles ABC and PQR:
$\angle A = \angle Q$
$\angle B = \angle R$
To Find:
Which side of $\triangle PQR$ should be equal to side AB of $\triangle ABC$ for congruence.
Solution:
In $\triangle ABC$, the side AB is included between the angles $\angle A$ and $\angle B$.
We are given that $\angle A = \angle Q$ and $\angle B = \angle R$.
For two triangles to be congruent by the ASA (Angle-Side-Angle) congruence criterion, two angles and the included side of one triangle must be equal to two corresponding angles and the included side of the other triangle.
The angles $\angle A$ and $\angle B$ in $\triangle ABC$ correspond to angles $\angle Q$ and $\angle R$ in $\triangle PQR$ respectively.
The side included between $\angle A$ and $\angle B$ in $\triangle ABC$ is AB.
The side included between the corresponding angles $\angle Q$ and $\angle R$ in $\triangle PQR$ is QR.
Therefore, for $\triangle ABC$ and $\triangle PQR$ to be congruent by the ASA criterion, the side AB of $\triangle ABC$ must be equal to the side QR of $\triangle PQR$.
If AB = QR, then by ASA congruence criterion, $\triangle ABC \cong \triangle QRP$.
Reason:
The reason is the ASA (Angle-Side-Angle) congruence criterion, which states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
Question 2. In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆ PQR should be equal to side BC of ∆ ABC so that the two triangles are congruent? Give reason for your answer.
Answer:
Given:
In $\triangle ABC$ and $\triangle PQR$, we are given two pairs of equal angles:
$\angle A = \angle Q$
... (i)
$\angle B = \angle R$
... (ii)
To Find:
Which side of $\triangle PQR$ must be equal to side BC of $\triangle ABC$ for the two triangles to be congruent.
Solution:
For the two triangles to be congruent, we can use either the ASA (Angle-Side-Angle) or the AAS (Angle-Angle-Side) congruence rule. Both rules require us to identify the correct corresponding parts.
First, let's establish the full correspondence of angles. By the angle sum property of a triangle, if two angles of one triangle are equal to two angles of another, their third angles must also be equal.
In $\triangle ABC$: $\angle C = 180^\circ - (\angle A + \angle B)$
In $\triangle PQR$: $\angle P = 180^\circ - (\angle Q + \angle R)$
Since $\angle A = \angle Q$ and $\angle B = \angle R$, it follows that:
$\angle C = \angle P$
... (iii)
So, the correspondence between the vertices is: A ↔ Q, B ↔ R, and C ↔ P.
The question specifies that we must use the side BC from $\triangle ABC$. To find its corresponding side in $\triangle PQR$, we look at the vertices that form the side.
Side BC is formed by vertices B and C.
The corresponding vertices in $\triangle PQR$ are R and P.
Therefore, the side corresponding to BC is RP (or PR).
Thus, for the triangles to be congruent, the side BC must be equal to the side PR.
Reason:
This conclusion is based on the congruence rules:
1. Using the ASA Congruence Rule: The ASA rule requires the side to be included between the two angles. In $\triangle ABC$, the side BC is included between $\angle B$ and $\angle C$. The corresponding parts in $\triangle PQR$ are $\angle R$, $\angle P$, and the included side PR. Therefore, if we are given $\angle B = \angle R$, $\angle C = \angle P$, and we set BC = PR, the triangles are congruent by ASA.
2. Using the AAS Congruence Rule: The AAS rule uses a non-included side. In $\triangle ABC$, with respect to the given angles $\angle A$ and $\angle B$, the side BC is a non-included side (it is opposite to $\angle A$). The corresponding parts in $\triangle PQR$ are $\angle Q$, $\angle R$, and the non-included side opposite $\angle Q$, which is PR. Therefore, if we are given $\angle A = \angle Q$, $\angle B = \angle R$, and we set BC = PR, the triangles are congruent by AAS.
In both valid scenarios, the side BC must be equal to the side PR.
Question 3. “If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Answer:
Answer:
The statement is False.
Reason:
For congruence to be guaranteed when two sides and an angle are equal, the angle must be the included angle—that is, the angle formed between the two given sides. This specific condition is known as the SAS (Side-Angle-Side) Congruence Rule.
The statement in the question is general and simply says "an angle". It does not specify that the angle must be the included one. If the angle is not the included angle, the condition is known as SSA (Side-Side-Angle). The SSA condition is famously known as the "ambiguous case" because it does not guarantee congruence.
It is possible to construct two different triangles that share the same SSA measurements. For example, consider a triangle where you know the lengths of sides 'a' and 'b' and the measure of angle 'A' (which is opposite side 'a'). If angle 'A' is acute and side 'a' is shorter than side 'b' but long enough to reach the third side, it can often do so in two different places, creating two distinct triangles.
Since the statement does not specify the position of the angle, and since the SSA case does not ensure congruence, the general statement that "two sides and an angle" are sufficient is false.
Question 4. “If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Answer:
The statement is False.
Reason:
For two triangles to be congruent, the equal sides and angles must be corresponding parts. The congruence rules ASA (Angle-Side-Angle) and AAS (Angle-Angle-Side) are valid only when the side in one triangle corresponds to the side in the other triangle.
The statement as written is too general. It allows for a situation where the equal side in the first triangle does not correspond to the equal side in the second triangle. If the sides are not corresponding, congruence is not guaranteed, even if two pairs of angles are equal.
We can demonstrate this with a counterexample:
Counterexample:
Consider two right-angled triangles, $\triangle ABC$ and $\triangle PQR$.
In $\triangle ABC$:
- Let $\angle A = 90^\circ$, $\angle B = 60^\circ$, and $\angle C = 30^\circ$.
- Let the hypotenuse (side opposite the right angle) be BC = 10 cm.
In $\triangle PQR$:
- Let $\angle P = 60^\circ$, $\angle Q = 30^\circ$, and $\angle R = 90^\circ$.
- Let the side opposite $\angle Q$ be PR = 10 cm.
Now, let's check if these two triangles satisfy the condition "two angles and a side of one triangle are equal to two angles and a side of another triangle":
- Angle 1: $\angle B$ in $\triangle ABC$ ($60^\circ$) is equal to $\angle P$ in $\triangle PQR$ ($60^\circ$).
- Angle 2: $\angle C$ in $\triangle ABC$ ($30^\circ$) is equal to $\angle Q$ in $\triangle PQR$ ($30^\circ$).
- Side: Side BC in $\triangle ABC$ (10 cm) is equal to side PR in $\triangle PQR$ (10 cm).
The condition is satisfied. But are the triangles congruent?
For the triangles to be congruent, their corresponding sides must be equal. The correspondence is A↔R, B↔P, C↔Q.
- The hypotenuse of $\triangle ABC$ is BC = 10 cm.
- The hypotenuse of $\triangle PQR$ is the side opposite the right angle $\angle R$, which is PQ. In a 30-60-90 triangle, the hypotenuse is twice the length of the shortest side (the one opposite the 30° angle). Here, the side opposite the 30° angle ($\angle Q$) is PR = 10 cm. Therefore, the hypotenuse PQ = 2 * 10 = 20 cm.
Since the hypotenuse of $\triangle ABC$ is 10 cm and the hypotenuse of $\triangle PQR$ is 20 cm, the triangles are not congruent.
This counterexample shows that having two angles and a non-corresponding side equal does not guarantee congruence. Therefore, the original statement is false.
Question 5. Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
Answer:
Answer:
No, it is not possible to construct a triangle with side lengths 4 cm, 3 cm, and 7 cm.
Reason:
For any three lengths to form a triangle, they must satisfy the Triangle Inequality Theorem.
This theorem states that the sum of the lengths of any two sides of a triangle must be strictly greater than the length of the third side.
Let the given side lengths be $a = 4$ cm, $b = 3$ cm, and $c = 7$ cm.
We check the triangle inequality for all pairs of sides:
1. $a + b > c$
$4 + 3 > 7$
$7 > 7$
This inequality is false, as 7 is not strictly greater than 7.
2. $a + c > b$
$4 + 7 > 3$
$11 > 3$
This inequality is true.
3. $b + c > a$
$3 + 7 > 4$
$10 > 4$
This inequality is true.
Since the first condition of the triangle inequality ($a + b > c$) is not satisfied, the given lengths cannot form a triangle.
Question 6. It is given that ∆ ABC ≅ ∆ RPQ. Is it true to say that BC = QR? Why?
Answer:
Answer:
No, it is not true to say that BC = QR.
Reason:
When two triangles are congruent, their corresponding parts are equal. This is known as CPCT (Corresponding Parts of Congruent Triangles).
The congruence statement $\triangle ABC \cong \triangle RPQ$ indicates the correspondence between the vertices of the two triangles in the order they are written.
This means:
Vertex A corresponds to Vertex R.
Vertex B corresponds to Vertex P.
Vertex C corresponds to Vertex Q.
Based on this correspondence, the corresponding sides are:
Side AB corresponds to side RP.
Side BC corresponds to side PQ.
Side AC corresponds to side RQ.
Therefore, by CPCT, BC is equal to PQ, not QR.
The side QR corresponds to the side AC.
Question 7. If ∆ PQR ≅ ∆ EDF, then is it true to say that PR = EF? Give reason for your answer.
Answer:
Yes, it is true to say that PR = EF.
Reason:
When two triangles are congruent, their corresponding parts are equal. This principle is known as CPCT (Corresponding Parts of Congruent Triangles).
The congruence statement $\triangle PQR \cong \triangle EDF$ establishes the correspondence between the vertices of the two triangles:
Vertex P corresponds to Vertex E.
Vertex Q corresponds to Vertex D.
Vertex R corresponds to Vertex F.
Based on this vertex correspondence, the corresponding sides are:
Side PQ corresponds to side ED.
Side QR corresponds to side DF.
Side PR corresponds to side EF.
Since PR and EF are corresponding sides in the given congruent triangles, their lengths must be equal by CPCT.
Question 8. In ∆ PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Answer:
Given:
In $\triangle PQR$, $\angle P = 70^\circ$ and $\angle R = 30^\circ$.
To Find:
The longest side of $\triangle PQR$.
Solution:
We are given two angles of $\triangle PQR$. To find the longest side, we need to determine the angle opposite each side. First, we find the third angle, $\angle Q$, using the angle sum property of a triangle.
The sum of the angles in any triangle is $180^\circ$.
So, $\angle P + \angle Q + \angle R = 180^\circ$.
Substituting the given values:
$70^\circ + \angle Q + 30^\circ = 180^\circ$
$100^\circ + \angle Q = 180^\circ$
$\angle Q = 180^\circ - 100^\circ$
$\angle Q = 80^\circ$
Now we have all three angles of the triangle:
$\angle P = 70^\circ$
$\angle Q = 80^\circ$
$\angle R = 30^\circ$
To find the longest side, we compare the measures of the three angles. The largest angle is $\angle Q = 80^\circ$.
The side opposite to angle $\angle Q$ in $\triangle PQR$ is the side connecting vertices P and R, which is PR.
According to the theorem relating angles and sides in a triangle, the side opposite the largest angle is the longest side.
Since $\angle Q$ is the largest angle, the side opposite to it, PR, is the longest side.
Reason:
In a triangle, the side opposite the largest angle is the longest side. We found that $\angle Q = 80^\circ$ is the largest angle in $\triangle PQR$, and the side opposite $\angle Q$ is PR.
Question 9. AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2 AD? Give reason for your answer.
Answer:
Answer:
Yes, the statement is True.
Given:
AD is a median of $\triangle ABC$. This means D is the midpoint of side BC.
To Prove:
AB + BC + CA $> 2$ AD
Proof:
In a triangle, the sum of the lengths of any two sides is always greater than the length of the third side. This is known as the Triangle Inequality Theorem.
Consider $\triangle ABD$. Applying the Triangle Inequality Theorem:
$AB + BD > AD$
AB + BD $> $ AD
... (i)
Now consider $\triangle ACD$. Applying the Triangle Inequality Theorem:
$AC + CD > AD$
AC + CD $> $ AD
... (ii)
Since AD is the median to BC, D is the midpoint of BC. Therefore, BD = CD.
Adding inequality (i) and inequality (ii):
$(AB + BD) + (AC + CD) > AD + AD$
$AB + AC + BD + CD > 2 AD$
Since D is the midpoint of BC, $BD + CD = BC$.
Substitute $BD + CD$ with BC:
$AB + AC + BC > 2 AD$
Rearranging the terms on the left side:
$AB + BC + CA > 2 AD$
This proves the statement.
Reason:
The reason is the Triangle Inequality Theorem, applied to the two triangles formed by the median ( $\triangle ABD$ and $\triangle ACD$), and the fact that the median divides the side into two equal parts.
Question 10. M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2AM? Give reason for your answer.
Answer:
Answer:
Yes, the statement is True.
Given:
M is a point on side BC of $\triangle ABC$. AM is the angle bisector of $\angle BAC$.
To Prove:
Perimeter of $\triangle ABC$ $> 2$ AM
i.e., AB + BC + CA $> 2$ AM
Proof:
In any triangle, the sum of the lengths of any two sides is always greater than the length of the third side. This is the Triangle Inequality Theorem.
Consider $\triangle ABM$. Applying the Triangle Inequality Theorem:
AB + BM $> $ AM
... (i)
Now consider $\triangle ACM$. Applying the Triangle Inequality Theorem:
AC + CM $> $ AM
... (ii)
Adding inequality (i) and inequality (ii):
$(AB + BM) + (AC + CM) > AM + AM$
$AB + AC + BM + CM > 2 AM$
Since M is a point on the side BC, the lengths BM and CM add up to the length of the side BC.
$BM + CM = BC$
Substitute $BM + CM$ with BC in the combined inequality:
$AB + AC + BC > 2 AM$
The expression $AB + BC + AC$ represents the perimeter of $\triangle ABC$.
Therefore, Perimeter of $\triangle ABC$ $> 2$ AM.
Note: The fact that AM is an angle bisector is not necessary for this inequality to hold. This inequality is true for any line segment AM where M is a point on BC.
Reason:
The statement is true based on the application of the Triangle Inequality Theorem to the two triangles ($\triangle ABM$ and $\triangle ACM$) formed by the line segment AM and the sides AB and AC, and the property that BM + CM = BC when M is a point on the segment BC.
Question 11. Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Answer:
Answer:
No, it is not possible to construct a triangle with side lengths 9 cm, 7 cm, and 17 cm.
Reason:
For any three lengths to form a triangle, they must satisfy the Triangle Inequality Theorem.
This theorem states that the sum of the lengths of any two sides of a triangle must be strictly greater than the length of the third side.
Let the given side lengths be $a = 9$ cm, $b = 7$ cm, and $c = 17$ cm.
We check the triangle inequality for all pairs of sides:
1. $a + b > c$
$9 + 7 > 17$
$16 > 17$
This inequality is false, as 16 is not strictly greater than 17.
Since one of the inequalities required by the Triangle Inequality Theorem is not satisfied, the given lengths cannot form a triangle.
We can also check the other two inequalities for completeness:
2. $a + c > b$
$9 + 17 > 7$
$26 > 7$
This inequality is true.
3. $b + c > a$
$7 + 17 > 9$
$24 > 9$
This inequality is true.
However, all three inequalities must be true for a triangle to be formed. Since $9 + 7 > 17$ is false, the triangle cannot be constructed.
Question 12. Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Answer:
Answer:
Yes, it is possible to construct a triangle with side lengths 8 cm, 7 cm, and 4 cm.
Reason:
For any three lengths to form a triangle, they must satisfy the Triangle Inequality Theorem.
This theorem states that the sum of the lengths of any two sides of a triangle must be strictly greater than the length of the third side.
Let the given side lengths be $a = 8$ cm, $b = 7$ cm, and $c = 4$ cm.
We check the triangle inequality for all pairs of sides:
1. $a + b > c$
$8 + 7 > 4$
$15 > 4$
This inequality is true.
2. $a + c > b$
$8 + 4 > 7$
$12 > 7$
This inequality is true.
3. $b + c > a$
$7 + 4 > 8$
$11 > 8$
This inequality is true.
Since the sum of the lengths of any two sides is greater than the length of the third side in all three cases, the given lengths satisfy the Triangle Inequality Theorem. Therefore, a triangle can be constructed with these side lengths.
Sample Question 1 to 3 (Before Exercise 7.3)
Sample Question 1: In Fig 7.1, PQ = PR and ∠Q = ∠R. Prove that ∆ PQS ≅ ∆ PRT.

Answer:
Given:
In the given figure, we have a triangle PQR with points S on PR and T on PQ.
We are given the following conditions:
PQ = PR
... (i)
$\angle Q = \angle R$
... (ii)
To Prove:
The triangle PQS is congruent to the triangle PRT.
$\triangle PQS \cong \triangle PRT$
Proof:
We will compare the two triangles, $\triangle PQS$ and $\triangle PRT$, and check for congruence using the given information.
In $\triangle PQS$ and $\triangle PRT$:
1. Consider the angle at vertex P. This angle, $\angle QPS$ (which is the same as $\angle RPT$), is common to both triangles.
$\angle QPS = \angle RPT$
[Common Angle]
2. We are given that the side PQ is equal to the side PR.
PQ = PR
[Given]
3. We are also given that $\angle Q$ is equal to $\angle R$. In the context of our two triangles, this means $\angle PQS = \angle PRT$.
$\angle PQS = \angle PRT$
[Given]
Now, let's see which congruence rule applies. We have established that two angles and the included side of $\triangle PQS$ are equal to the corresponding two angles and the included side of $\triangle PRT$.
- Angle: $\angle QPS = \angle RPT$
- Side (included): PQ = PR
- Angle: $\angle PQS = \angle PRT$
Therefore, by the ASA (Angle-Side-Angle) congruence rule, the two triangles are congruent.
$\triangle PQS \cong \triangle PRT$
[By ASA congruence rule]
Hence, proved.
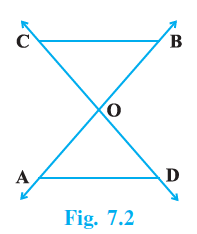
Sample Question 2: In Fig.7.2, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the midpoint of both the line-segments AB and CD.
Answer:
Given:
In the given figure, two line segments AB and CD intersect at a point O.
We are given the following conditions:
BC || DA
BC = DA
To Prove:
O is the midpoint of both the line-segments AB and CD. This means we need to prove:
1. OA = OB
2. OC = OD
Proof:
To prove that O is the midpoint of the segments, we will first prove that the triangle $\triangle OBC$ is congruent to the triangle $\triangle OAD$.
Let's consider $\triangle OBC$ and $\triangle OAD$.
Step 1: Identify equal angles using the parallel lines.
We are given that BC || DA.
Consider CD as a transversal intersecting these parallel lines. The angles $\angle OCB$ and $\angle ODA$ form a pair of alternate interior angles. Therefore, they are equal.
$\angle OCB = \angle ODA$
[Alternate Interior Angles]
Now, consider AB as another transversal intersecting the parallel lines BC and DA. The angles $\angle OBC$ and $\angle OAD$ form another pair of alternate interior angles. Therefore, they are also equal.
$\angle OBC = \angle OAD$
[Alternate Interior Angles]
Step 2: Compare the two triangles for congruence.
In $\triangle OBC$ and $\triangle OAD$:
1. Angle: $\angle OBC = \angle OAD$ (Proved above)
2. Side: BC = DA (Given)
3. Angle: $\angle OCB = \angle ODA$ (Proved above)
We have two angles and the included side of $\triangle OBC$ equal to the corresponding two angles and the included side of $\triangle OAD$.
Therefore, by the ASA (Angle-Side-Angle) congruence rule, the two triangles are congruent.
$\triangle OBC \cong \triangle OAD$
[By ASA congruence rule]
Step 3: Conclude using CPCTC.
Since the two triangles are congruent, their corresponding parts must be equal. This is known as CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
The correspondence is O ↔ O, B ↔ A, and C ↔ D.
From this correspondence, we can state:
OB = OA
[By CPCTC]
OC = OD
[By CPCTC]
The condition OB = OA means that O is the midpoint of the line segment AB.
The condition OC = OD means that O is the midpoint of the line segment CD.
Thus, we have shown that O is the midpoint of both the line-segments AB and CD.
Hence, proved.
Sample Question 3: In Fig.7.3, PQ > PR and QS and RS are the bisectors of ∠Q and ∠R, respectively. Show that SQ > SR.

Answer:
Given:
In the triangle $\triangle PQR$, we are given:
PQ > PR
QS is the bisector of $\angle Q$.
RS is the bisector of $\angle R$.
To Prove:
SQ > SR
Proof:
The proof relies on the relationship between the lengths of sides and the measures of their opposite angles in a triangle.
Step 1: Relate the sides and angles in the main triangle, $\triangle PQR$.
We are given that side PQ > side PR.
A fundamental theorem in triangle geometry states that the angle opposite the longer side is larger.
- The angle opposite to the side PQ is $\angle R$.
- The angle opposite to the side PR is $\angle Q$.
Since PQ > PR, it follows that the angle opposite PQ must be greater than the angle opposite PR.
$\angle R > \angle Q$
... (i)
Step 2: Use the angle bisector information.
We are given that QS is the bisector of $\angle Q$ and RS is the bisector of $\angle R$. This means:
$\angle SQR = \frac{1}{2} \angle Q$
$\angle SRQ = \frac{1}{2} \angle R$
From our result in Step 1 (inequality (i)), we have $\angle R > \angle Q$.
If we multiply both sides of this inequality by $\frac{1}{2}$, the inequality remains true:
$\frac{1}{2} \angle R > \frac{1}{2} \angle Q$
Substituting the bisected angle names into this inequality, we get:
$\angle SRQ > \angle SQR$
Step 3: Relate the angles and sides in the smaller triangle, $\triangle SQR$.
Now, let's focus on the triangle $\triangle SQR$. We have just shown that in this triangle, $\angle SRQ > \angle SQR$.
The converse of the theorem used in Step 1 states that the side opposite the larger angle is longer.
- The side opposite to the angle $\angle SRQ$ is SQ.
- The side opposite to the angle $\angle SQR$ is SR.
Since $\angle SRQ > \angle SQR$, it follows that the side opposite $\angle SRQ$ must be longer than the side opposite $\angle SQR$.
SQ > SR
Hence, proved.
Exercise 7.3
Question 1. ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
Answer:
Given:
$\triangle ABC$ is an isosceles triangle.
AB = AC
BD is a median to the side AC. This means D is the midpoint of AC, so AD = DC.
CE is a median to the side AB. This means E is the midpoint of AB, so AE = EB.
To Prove:
The two medians are equal in length.
BD = CE
Proof:
To prove that the medians BD and CE are equal, we will prove the congruence of two triangles that contain these medians as sides. Let's consider $\triangle ABD$ and $\triangle ACE$.
Step 1: Relate the segments AE and AD.
We are given that AB = AC.
Taking half of both sides, we get:
$\frac{1}{2} AB = \frac{1}{2} AC$
Since E is the midpoint of AB, we have $AE = \frac{1}{2} AB$.
Since D is the midpoint of AC, we have $AD = \frac{1}{2} AC$.
Therefore, substituting these into the equation above, we get:
AE = AD
... (i)
Step 2: Compare $\triangle ABD$ and $\triangle ACE$ for congruence.
In $\triangle ABD$ and $\triangle ACE$:
1. Side: AB = AC (Given)
2. Angle: $\angle BAD = \angle CAE$ (This is the angle $\angle A$, which is common to both triangles)
3. Side: AD = AE (Proved in Step 1, from equation (i))
We have two sides and the included angle of $\triangle ABD$ equal to the corresponding two sides and the included angle of $\triangle ACE$.
Therefore, by the SAS (Side-Angle-Side) congruence rule, the two triangles are congruent.
$\triangle ABD \cong \triangle ACE$
[By SAS congruence rule]
Step 3: Conclude using CPCTC.
Since the two triangles are congruent, their corresponding parts must be equal (CPCTC).
The side BD in $\triangle ABD$ corresponds to the side CE in $\triangle ACE$.
Therefore:
BD = CE
[By CPCTC]
Hence, proved.
Alternate Solution (using $\triangle EBC$ and $\triangle DCB$):
1. Since AB = AC, the angles opposite to these sides are equal: $\angle ABC = \angle ACB$.
2. We have $EB = \frac{1}{2}AB$ and $DC = \frac{1}{2}AC$. Since AB = AC, it follows that $EB = DC$.
Now, in $\triangle EBC$ and $\triangle DCB$:
- Side: EB = DC (Proved above)
- Angle: $\angle EBC = \angle DCB$ (Proved above, since $\angle ABC = \angle ACB$)
- Side: BC = CB (Common side)
By the SAS congruence rule, $\triangle EBC \cong \triangle DCB$.
By CPCTC, the corresponding sides CE and BD must be equal.
CE = BD
Hence, proved.
Question 2. In Fig.7.4, D and E are points on side BC of a ∆ ABC such that BD = CE and AD = AE. Show that ∆ ABD ≅ ∆ ACE.
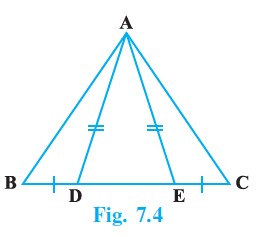
Answer:
Given:
In $\triangle ABC$, D and E are points on the side BC.
We are given the following conditions:
BD = CE
... (i)
AD = AE
... (ii)
To Prove:
$\triangle ABD \cong \triangle ACE$
Proof:
To prove that $\triangle ABD \cong \triangle ACE$, we need to establish the equality of corresponding sides and angles to satisfy a congruence criterion (like SSS, SAS, ASA, AAS).
Step 1: Use the properties of $\triangle ADE$.
First, let's consider the triangle $\triangle ADE$.
We are given that AD = AE. A triangle with two equal sides is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are also equal.
- The angle opposite side AE is $\angle ADE$.
- The angle opposite side AD is $\angle AED$.
Therefore, we can conclude:
$\angle ADE = \angle AED$
[Angles opposite to equal sides] ... (iii)
Step 2: Relate the angles of $\triangle ADE$ to the angles of $\triangle ABD$ and $\triangle ACE$.
The angles $\angle ADB$ and $\angle ADE$ form a linear pair on the straight line BC. Therefore, their sum is $180^\circ$.
$\angle ADB + \angle ADE = 180^\circ$
[Linear Pair]
This means $\angle ADB = 180^\circ - \angle ADE$.
Similarly, the angles $\angle AEC$ and $\angle AED$ form a linear pair on the straight line BC.
$\angle AEC + \angle AED = 180^\circ$
[Linear Pair]
This means $\angle AEC = 180^\circ - \angle AED$.
From equation (iii), we know that $\angle ADE = \angle AED$. Therefore, their supplements must also be equal:
$180^\circ - \angle ADE = 180^\circ - \angle AED$
This implies:
$\angle ADB = \angle AEC$
... (iv)
Step 3: Compare $\triangle ABD$ and $\triangle ACE$ for congruence.
Let's list the equal parts we have found for $\triangle ABD$ and $\triangle ACE$:
- AD = AE (Side) [Given]
- $\angle ADB = \angle AEC$ (Angle) [Proved]
- BD = CE (Side) [Given]
In $\triangle ABD$, the angle between sides AD and BD is $\angle ADB$.
In $\triangle ACE$, the angle between sides AE and CE is $\angle AEC$.
So, we have two sides and the included angle of one triangle equal to the corresponding two sides and included angle of the other triangle.
Therefore, by the SAS (Side-Angle-Side) congruence rule, the two triangles are congruent.
$\triangle ABD \cong \triangle ACE$
[By SAS congruence rule]
Hence, proved.
Question 3. CDE is an equilateral triangle formed on a side CD of a square ABCD (Fig.7.5). Show that ∆ ADE ≅ ∆ BCE.
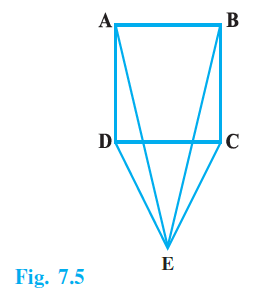
Answer:
Given:
ABCD is a square.
CDE is an equilateral triangle formed on the side CD of the square.
To Prove:
$\triangle ADE \cong \triangle BCE$
Proof:
We need to prove the congruence of $\triangle ADE$ and $\triangle BCE$. We will do this by establishing the equality of their corresponding sides and angles.
Step 1: Use the properties of the square ABCD.
Since ABCD is a square, all its sides are equal in length, and all its interior angles are right angles ($90^\circ$).
AD = BC = CD = AB
... (i)
$\angle ADC = \angle BCD = 90^\circ$
... (ii)
Step 2: Use the properties of the equilateral triangle CDE.
Since CDE is an equilateral triangle, all its sides are equal in length, and all its interior angles are $60^\circ$.
CD = DE = CE
... (iii)
$\angle EDC = \angle DCE = 60^\circ$
... (iv)
Step 3: Combine the properties to find equal sides and angles for the required triangles.
From (i) and (iii), we can relate the sides of the square and the triangle:
AD = CD and CD = DE, which implies AD = DE.
BC = CD and CD = CE, which implies BC = CE.
Now, let's find the measure of the angles $\angle ADE$ and $\angle BCE$.
From the figure, $\angle ADE$ is the sum of $\angle ADC$ and $\angle EDC$.
$\angle ADE = \angle ADC + \angle EDC$
Using values from (ii) and (iv):
$\angle ADE = 90^\circ + 60^\circ = 150^\circ$.
Similarly, $\angle BCE$ is the sum of $\angle BCD$ and $\angle DCE$.
$\angle BCE = \angle BCD + \angle DCE$
Using values from (ii) and (iv):
$\angle BCE = 90^\circ + 60^\circ = 150^\circ$.
Therefore, we have shown that $\angle ADE = \angle BCE$.
Step 4: Compare $\triangle ADE$ and $\triangle BCE$ for congruence.
In $\triangle ADE$ and $\triangle BCE$:
1. Side: AD = BC (Sides of a square, from (i))
2. Angle: $\angle ADE = \angle BCE$ (Both are $150^\circ$, proved above)
3. Side: DE = CE (Sides of an equilateral triangle, from (iii))
We have two sides and the included angle of $\triangle ADE$ equal to the corresponding two sides and the included angle of $\triangle BCE$.
Therefore, by the SAS (Side-Angle-Side) congruence rule, the two triangles are congruent.
$\triangle ADE \cong \triangle BCE$
[By SAS congruence rule]
Hence, proved.
Question 4. In Fig.7.6, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that ∆ ABC ≅ ∆ DEF.

Answer:
Given:
In the given figure, we have two triangles, $\triangle ABC$ and $\triangle DEF$.
The following conditions are given:
BA ⊥ AC, which means $\angle A = 90^\circ$
DE ⊥ DF, which means $\angle D = 90^\circ$
BA = DE
... (i)
BF = EC
... (ii)
To Prove:
$\triangle ABC \cong \triangle DEF$
Proof:
We need to prove the congruence of the two right-angled triangles, $\triangle ABC$ and $\triangle DEF$. The most common congruence rule for right-angled triangles is the RHS (Right angle-Hypotenuse-Side) rule. Let's see if we can use it.
Step 1: Establish the equality of the hypotenuses.
The hypotenuse of $\triangle ABC$ is BC.
The hypotenuse of $\triangle DEF$ is EF.
We are given that BF = EC.
From the figure, we can see that the segment BC is composed of BF and FC, and the segment EF is composed of EC and FC.
Let's add the length of the segment FC to both sides of the given equality (ii):
BF + FC = EC + FC
By the Segment Addition Postulate, BF + FC = BC.
Similarly, EC + FC = EF.
Therefore, we can conclude that:
BC = EF
... (iii)
This shows that the hypotenuses of the two triangles are equal.
Step 2: Compare $\triangle ABC$ and $\triangle DEF$ for congruence using the RHS rule.
In the right-angled triangles $\triangle ABC$ and $\triangle DEF$:
1. Right angle: $\angle A = \angle D = 90^\circ$ (Given)
2. Hypotenuse: BC = EF (Proved in Step 1, from (iii))
3. Side: BA = DE (Given in (i))
We have shown that the hypotenuse and one side of the right-angled triangle $\triangle ABC$ are equal to the hypotenuse and the corresponding side of the right-angled triangle $\triangle DEF$.
Therefore, by the RHS (Right angle-Hypotenuse-Side) congruence rule, the two triangles are congruent.
$\triangle ABC \cong \triangle DEF$
[By RHS congruence rule]
Hence, proved.
Question 5. Q is a point on the side SR of a ∆ PSR such that PQ = PR. Prove that PS > PQ.
Answer:
Given:
In a triangle $\triangle PSR$, Q is a point on the side SR.
A line segment PQ is drawn such that it is equal to PR.
PQ = PR
To Prove:
PS > PQ
Proof:
The proof relies on two key geometric theorems: the property of isosceles triangles and the exterior angle theorem.
Step 1: Use the property of the isosceles triangle $\triangle PQR$.
We are given that in $\triangle PQR$, the sides PQ and PR are equal.
PQ = PR
[Given]
In a triangle, the angles opposite to equal sides are equal.
- The angle opposite to side PR is $\angle PQR$.
- The angle opposite to side PQ is $\angle PRQ$.
Therefore, we can conclude that:
$\angle PQR = \angle PRQ$
[Angles opposite equal sides are equal] ... (i)
Step 2: Apply the Exterior Angle Theorem to $\triangle PSQ$.
Now, let's consider the triangle $\triangle PSQ$.
The angle $\angle PQR$ is an exterior angle to $\triangle PSQ$ because the side SQ is extended to R.
The Exterior Angle Theorem states that an exterior angle of a triangle is greater than either of its interior opposite angles.
The interior opposite angles to the exterior angle $\angle PQR$ are $\angle PSQ$ (or $\angle PSR$) and $\angle SPQ$.
Therefore, we have:
$\angle PQR > \angle PSQ$
[Exterior Angle Theorem]
Step 3: Relate the angles inside $\triangle PSR$.
From equation (i), we know that $\angle PQR = \angle PRQ$.
Substituting this into the inequality from Step 2, we get:
$\angle PRQ > \angle PSQ$
In the context of the larger triangle $\triangle PSR$, $\angle PRQ$ is the same as $\angle PRS$, and $\angle PSQ$ is the same as $\angle PSR$. So, in $\triangle PSR$, we have:
$\angle PRS > \angle PSR$
Step 4: Relate the sides in $\triangle PSR$.
In any triangle, the side opposite the larger angle is longer.
In $\triangle PSR$:
- The side opposite to $\angle PRS$ is PS.
- The side opposite to $\angle PSR$ is PR.
Since $\angle PRS > \angle PSR$, it follows that:
PS > PR
Finally, we use the given condition that PR = PQ. Substituting this into our result:
PS > PQ
Hence, proved.
Question 6. S is any point on side QR of a ∆ PQR. Show that: PQ + QR + RP > 2 PS.
Answer:
Given:
S is any point on the side QR of a triangle $\triangle PQR$.
A line segment PS is drawn.
To Prove:
The perimeter of $\triangle PQR$ is greater than twice the length of the segment PS.
That is, PQ + QR + RP > 2 PS.
Proof:
The proof is based on the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
The line segment PS divides the main triangle $\triangle PQR$ into two smaller triangles: $\triangle PQS$ and $\triangle PRS$. We will apply the Triangle Inequality Theorem to each of these smaller triangles.
Step 1: Apply the Triangle Inequality Theorem to $\triangle PQS$.
In $\triangle PQS$, the sum of the sides PQ and QS must be greater than the third side, PS.
PQ + QS > PS
... (i)
Step 2: Apply the Triangle Inequality Theorem to $\triangle PRS$.
In $\triangle PRS$, the sum of the sides PR (which is the same as RP) and SR must be greater than the third side, PS.
RP + SR > PS
... (ii)
Step 3: Combine the two inequalities.
Now, we add the two inequalities, (i) and (ii). We add the left-hand sides together and the right-hand sides together.
(PQ + QS) + (RP + SR) > PS + PS
Rearranging the terms on the left side by grouping the sides of the original triangle:
PQ + RP + (QS + SR) > 2 PS
Since S is a point on the side QR, the sum of the lengths of the segments QS and SR is equal to the length of the entire side QR.
QS + SR = QR
Substituting this into our combined inequality, we get:
PQ + RP + QR > 2 PS
Finally, rearranging the terms to match the required statement:
PQ + QR + RP > 2 PS
Hence, proved.
Question 7. D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
Answer:
Given:
In a triangle $\triangle ABC$, we have AB = AC.
D is any point on the side AC.
To Prove:
CD < BD
Proof:
The proof relies on the relationship between sides and their opposite angles within a triangle.
Step 1: Analyze the given isosceles triangle $\triangle ABC$.
We are given that in $\triangle ABC$, the sides are equal:
AB = AC
[Given]
A fundamental property of triangles states that if two sides of a triangle are equal, then the angles opposite to these equal sides are also equal.
- The angle opposite side AC is $\angle ABC$.
- The angle opposite side AB is $\angle ACB$.
Therefore, we can conclude that:
$\angle ABC = \angle ACB$
[Angles opposite equal sides] ... (i)
Step 2: Relate the angles of $\triangle ABC$ to the angles of $\triangle BDC$.
Since D is a point on the side AC, the ray BD lies in the interior of the angle $\angle ABC$.
This means that the angle $\angle ABC$ is the sum of two smaller angles, $\angle ABD$ and $\angle DBC$.
$\angle ABC = \angle ABD + \angle DBC$
Since $\angle ABD$ is a part of a triangle, its measure is greater than zero. This implies that the whole angle $\angle ABC$ must be greater than its part, $\angle DBC$.
$\angle ABC > \angle DBC$
... (ii)
Now, let's combine the results from (i) and (ii). From (i), we know $\angle ABC = \angle ACB$. We can substitute $\angle ACB$ into the inequality (ii):
$\angle ACB > \angle DBC$
Step 3: Apply the side-angle relationship in $\triangle BDC$.
Let us now focus on the triangle $\triangle BDC$.
In $\triangle BDC$, the angle $\angle ACB$ is the same as $\angle BCD$. So, our inequality from Step 2 can be written as:
$\angle BCD > \angle DBC$
Another key theorem in triangle geometry states that the side opposite the larger angle is longer.
In $\triangle BDC$:
- The side opposite to the angle $\angle BCD$ is BD.
- The side opposite to the angle $\angle DBC$ is CD.
Since $\angle BCD > \angle DBC$, the side opposite $\angle BCD$ must be longer than the side opposite $\angle DBC$.
BD > CD
This can also be written as:
CD < BD
Hence, proved.
Question 8. In Fig. 7.7, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.

Answer:
Given:
Two parallel lines, l and m.
l || m
M is the midpoint of a line segment AB, where A is on line l and B is on line m.
AM = BM
CD is another line segment with endpoint C on line l and endpoint D on line m, and this segment also passes through M.
To Prove:
M is also the midpoint of the line segment CD.
That is, CM = DM.
Proof:
To prove that CM = DM, we will first prove the congruence of the two triangles formed by the intersecting line segments, which are $\triangle AMC$ and $\triangle BMD$.
Let's consider $\triangle AMC$ and $\triangle BMD$.
Step 1: Identify equal angles using the parallel lines and intersecting lines.
Since line l is parallel to line m, and the line segment AB acts as a transversal.
The angles $\angle CAM$ and $\angle DBM$ (or $\angle CAB$ and $\angle DBA$) are alternate interior angles. Therefore, they are equal.
$\angle CAM = \angle DBM$
[Alternate Interior Angles]
Now, consider the intersecting line segments AB and CD at point M.
The angles $\angle AMC$ and $\angle BMD$ are vertically opposite angles. Therefore, they are equal.
$\angle AMC = \angle BMD$
[Vertically Opposite Angles]
Step 2: Compare $\triangle AMC$ and $\triangle BMD$ for congruence.
In $\triangle AMC$ and $\triangle BMD$:
1. Angle: $\angle CAM = \angle DBM$ (Proved above)
2. Side: AM = BM (Given that M is the midpoint of AB)
3. Angle: $\angle AMC = \angle BMD$ (Proved above)
We have two angles and the included side of $\triangle AMC$ equal to the corresponding two angles and the included side of $\triangle BMD$.
Therefore, by the ASA (Angle-Side-Angle) congruence rule, the two triangles are congruent.
$\triangle AMC \cong \triangle BMD$
[By ASA congruence rule]
Step 3: Conclude using CPCTC.
Since the two triangles are congruent, their corresponding parts must be equal (CPCTC).
The side CM in $\triangle AMC$ corresponds to the side DM in $\triangle BMD$.
Therefore:
CM = DM
[By CPCTC]
Since CM = DM, M is the midpoint of the line segment CD.
Hence, proved.
Question 9. Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Answer:
Given:
An isosceles triangle $\triangle ABC$ with AB = AC.
BO is the bisector of $\angle B$.
CO is the bisector of $\angle C$.
The bisectors intersect at point O.
The line segment BO is produced (extended) to a point M.
To Prove:
$\angle MOC = \angle ABC$
Proof:
Step 1: Use the property of the isosceles triangle $\triangle ABC$.
Since $\triangle ABC$ is an isosceles triangle with AB = AC, the angles opposite to these equal sides are also equal.
$\angle ABC = \angle ACB$
[Angles opposite equal sides] ... (i)
Step 2: Use the angle bisector information.
BO is the bisector of $\angle ABC$, so:
$\angle OBC = \frac{1}{2} \angle ABC$
CO is the bisector of $\angle ACB$, so:
$\angle OCB = \frac{1}{2} \angle ACB$
Since $\angle ABC = \angle ACB$ from (i), their halves must also be equal:
$\frac{1}{2} \angle ABC = \frac{1}{2} \angle ACB \implies \angle OBC = \angle OCB$
Step 3: Apply the Exterior Angle Theorem to $\triangle BOC$.
The line segment BOM is a straight line. Therefore, the angle $\angle MOC$ is an exterior angle to the triangle $\triangle BOC$.
The Exterior Angle Theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles.
The interior opposite angles to the exterior angle $\angle MOC$ are $\angle OBC$ and $\angle OCB$.
$\angle MOC = \angle OBC + \angle OCB$
[Exterior Angle Theorem] ... (ii)
Step 4: Combine the results.
Now, we substitute the expressions for the bisected angles from Step 2 into equation (ii):
$\angle MOC = \left(\frac{1}{2} \angle ABC\right) + \left(\frac{1}{2} \angle ACB\right)$
$\angle MOC = \frac{1}{2} (\angle ABC + \angle ACB)$
From Step 1 (equation (i)), we know that $\angle ABC = \angle ACB$. So, we can replace $\angle ACB$ with $\angle ABC$ in the equation above:
$\angle MOC = \frac{1}{2} (\angle ABC + \angle ABC)$
$\angle MOC = \frac{1}{2} (2 \times \angle ABC)$
$\angle MOC = \angle ABC$
Hence, proved.
Question 10. Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC.
Answer:
Given:
An isosceles triangle $\triangle ABC$ with AB = AC.
BO is the bisector of $\angle B$.
CO is the bisector of $\angle C$.
The bisectors intersect at point O.
The side AB is extended to a point D, creating the external angle $\angle DBC$.
To Prove:
The external angle adjacent to $\angle ABC$ is equal to $\angle BOC$.
That is, $\angle DBC = \angle BOC$.
Proof:
Step 1: Use the property of the isosceles triangle $\triangle ABC$.
Since $\triangle ABC$ is an isosceles triangle with AB = AC, the angles opposite to these equal sides are also equal.
$\angle ABC = \angle ACB$
[Angles opposite equal sides] ... (i)
Step 2: Use the angle bisector information.
BO bisects $\angle ABC$, so $\angle OBC = \frac{1}{2} \angle ABC$.
CO bisects $\angle ACB$, so $\angle OCB = \frac{1}{2} \angle ACB$.
Since $\angle ABC = \angle ACB$, their halves are also equal: $\angle OBC = \angle OCB$.
Step 3: Apply the Angle Sum Property in $\triangle BOC$.
$\angle BOC + \angle OBC + \angle OCB = 180^\circ$
Substitute the expressions in terms of the main triangle's angles:
$\angle BOC + \frac{1}{2}\angle ABC + \frac{1}{2}\angle ACB = 180^\circ$
Since $\angle ABC = \angle ACB$, we can write:
$\angle BOC + \frac{1}{2}\angle ABC + \frac{1}{2}\angle ABC = 180^\circ$
$\angle BOC + \angle ABC = 180^\circ$
Isolating $\angle BOC$, we get:
$\angle BOC = 180^\circ - \angle ABC$
... (ii)
Step 4: Use the property of Linear Pair.
The side AB is extended to D, which means DBA is a straight line.
The angles $\angle DBC$ and $\angle ABC$ form a linear pair. Therefore, their sum is $180^\circ$.
$\angle DBC + \angle ABC = 180^\circ$
[Linear Pair]
Isolating the external angle $\angle DBC$, we get:
$\angle DBC = 180^\circ - \angle ABC$
... (iii)
Step 5: Compare the results.
From equation (ii), we found that $\angle BOC = 180^\circ - \angle ABC$.
From equation (iii), we found that $\angle DBC = 180^\circ - \angle ABC$.
Since both angles are equal to the same expression, they must be equal to each other.
$\angle DBC = \angle BOC$
Hence, proved.
Question 11. In Fig. 7.8, AD is the bisector of ∠BAC. Prove that AB > BD.
Answer:
Given:
In $\triangle ABC$, the line segment AD is the bisector of $\angle BAC$.
To Prove:
AB > BD
Proof:
To prove the inequality AB > BD, we will compare the angles opposite to these sides within the triangle $\triangle ABD$. The theorem we will use is: In a triangle, the side opposite the larger angle is longer.
Step 1: Use the property of the angle bisector.
Since AD is the bisector of $\angle BAC$, it divides the angle into two equal parts.
$\angle BAD = \angle CAD$
... (i)
Step 2: Use the Exterior Angle Theorem.
Let's consider the triangle $\triangle ADC$.
The angle $\angle ADB$ is an exterior angle to $\triangle ADC$.
The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of its two interior opposite angles. The interior opposite angles to $\angle ADB$ are $\angle CAD$ and $\angle ACD$ (or $\angle C$).
$\angle ADB = \angle CAD + \angle C$
Since $\angle C$ is an angle of a triangle, its measure is positive ($\angle C > 0^\circ$).
This means that the exterior angle $\angle ADB$ must be greater than the interior opposite angle $\angle CAD$.
$\angle ADB > \angle CAD$
... (ii)
Step 3: Combine the results.
From equation (i), we know that $\angle CAD = \angle BAD$. We can substitute this into our inequality (ii):
$\angle ADB > \angle BAD$
Step 4: Apply the side-angle relationship in $\triangle ABD$.
Now, we focus on the triangle $\triangle ABD$. We have just shown that in this triangle, the angle $\angle ADB$ is greater than the angle $\angle BAD$.
In $\triangle ABD$:
- The side opposite to the angle $\angle ADB$ is AB.
- The side opposite to the angle $\angle BAD$ is BD.
Since the side opposite the larger angle is longer, and $\angle ADB > \angle BAD$, we can conclude that:
AB > BD
Hence, proved.
Sample Question 1 to 4 (Before Exercise 7.4)
Sample Question 1: In Fig. 7.9, ABC is a right triangle and right angled at B such that ∠BCA = 2 ∠BAC. Show that hypotenuse AC = 2 BC.

Answer:
Given:
In a right-angled triangle ABC, $\angle ABC = 90^\circ$.
$\angle BCA = 2 \angle BAC$
(Given)
To Prove:
Hypotenuse $AC = 2 BC$.
Construction Required:
Produce the side CB to a point D such that $BC = BD$. Join AD. The resulting figure is shown in the problem's diagram.
Proof:
First, let's determine the angles of $\triangle ABC$.
Let $\angle BAC = x$.
From the given information, $\angle BCA = 2x$.
In $\triangle ABC$, the sum of all angles is $180^\circ$.
$\angle BAC + \angle BCA + \angle ABC = 180^\circ$
$x + 2x + 90^\circ = 180^\circ$
$3x = 180^\circ - 90^\circ$
$3x = 90^\circ$
$x = \frac{90^\circ}{3}$
$x = 30^\circ$
Therefore, we have:
$\angle BAC = 30^\circ$
$\angle BCA = 2 \times 30^\circ = 60^\circ$
Now, consider $\triangle ABC$ and $\triangle ABD$.
BC = BD
(By Construction)
$\angle ABC = \angle ABD = 90^\circ$
(CD is a straight line)
AB = AB
(Common side)
Thus, by SAS (Side-Angle-Side) congruence criterion, $\triangle ABC \cong \triangle ABD$.
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
AC = AD
... (i)
$\angle BAC = \angle BAD$
... (ii)
Since $\angle BAC = 30^\circ$, it follows from (ii) that $\angle BAD = 30^\circ$.
Now, $\angle CAD = \angle BAC + \angle BAD = 30^\circ + 30^\circ = 60^\circ$.
In $\triangle ADC$, we have:
$\angle CAD = 60^\circ$
$\angle ACD = \angle BCA = 60^\circ$
The third angle, $\angle ADC$, can be found using the angle sum property:
$\angle ADC = 180^\circ - (\angle CAD + \angle ACD) = 180^\circ - (60^\circ + 60^\circ) = 60^\circ$.
Since all three angles of $\triangle ADC$ are $60^\circ$, it is an equilateral triangle.
Therefore, all its sides are equal: $AC = AD = CD$.
We know that $CD = CB + BD$.
By construction, $BD = BC$, so $CD = BC + BC = 2BC$.
Since $AC = CD$, we can conclude that:
$AC = 2BC$
Hence, proved.
Sample Question 2: Prove that if in two triangles two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, then the two triangles are congruent.
Answer:
This is a proof for the Angle-Side-Angle (ASA) congruence theorem.
Given:
Two triangles, $\triangle ABC$ and $\triangle DEF$, such that:
$\angle B = \angle E$
(Angle)
BC = EF
(Included Side)
$\angle C = \angle F$
(Angle)
To Prove:
$\triangle ABC \cong \triangle DEF$.
Proof:
To prove the congruence of the two triangles, we will consider the lengths of the sides AB and DE. There are three possible cases:
Case 1: Let AB = DE
In $\triangle ABC$ and $\triangle DEF$, we have:
AB = DE
(Assumption)
$\angle B = \angle E$
(Given)
BC = EF
(Given)
Thus, by the SAS (Side-Angle-Side) congruence criterion, $\triangle ABC \cong \triangle DEF$.
Case 2: Let AB > DE
If AB is greater than DE, we can choose a point P on the side AB such that $PB = DE$.
Now, consider $\triangle PBC$ and $\triangle DEF$.
PB = DE
(By Construction)
$\angle B = \angle E$
(Given)
BC = EF
(Given)
By the SAS congruence criterion, $\triangle PBC \cong \triangle DEF$.
Since the triangles are congruent, their corresponding parts are equal. Therefore, by CPCTC (Corresponding Parts of Congruent Triangles are Congruent):
$\angle PCB = \angle DFE$
However, it is given that:
$\angle ACB = \angle DFE$
From the above two statements, it must be that $\angle PCB = \angle ACB$.
This is only possible if the point P coincides with the point A. If P coincides with A, then $PB = AB$.
But we constructed $PB = DE$. Therefore, $AB = DE$.
This contradicts our initial assumption for this case (that AB > DE). So, this case is not possible.
Case 3: Let AB < DE
If AB is less than DE, we can choose a point M on the side DE such that $ME = AB$.
Now, consider $\triangle ABC$ and $\triangle MEF$.
AB = ME
(By Construction)
$\angle B = \angle E$
(Given)
BC = EF
(Given)
By the SAS congruence criterion, $\triangle ABC \cong \triangle MEF$.
By CPCTC, we have:
$\angle ACB = \angle MFE$
However, it is given that:
$\angle ACB = \angle DFE$
Therefore, it must be that $\angle MFE = \angle DFE$.
This is only possible if the ray FM coincides with the ray FD, which means point M must coincide with point D. If M coincides with D, then $ME = DE$.
But we constructed $ME = AB$. Therefore, $AB = DE$.
This contradicts our initial assumption for this case (that AB < DE). So, this case is not possible.
Since Case 2 and Case 3 are not possible, the only possibility is Case 1.
Thus, $AB = DE$, which leads to $\triangle ABC \cong \triangle DEF$.
Hence, the ASA congruence theorem is proved.
Sample Question 3: If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
Answer:
Given:
A triangle $\triangle ABC$ in which AD is the bisector of $\angle A$ and it also bisects the opposite side BC.
This means:
1. $\angle BAD = \angle CAD$ (AD bisects $\angle A$)
2. $BD = CD$ (D is the midpoint of BC)
To Prove:
The triangle $\triangle ABC$ is an isosceles triangle, i.e., $AB = AC$.
Construction Required:
Extend the line segment AD to a point E such that $AD = DE$. Join the point C to E.
Proof:
We consider the triangles $\triangle ABD$ and $\triangle ECD$.
AD = ED
(By Construction)
$\angle ADB = \angle EDC$
(Vertically opposite angles)
BD = CD
(Given, as D is the midpoint of BC)
Therefore, by the SAS (Side-Angle-Side) congruence criterion, we have:
$\triangle ABD \cong \triangle ECD$
Since the triangles are congruent, their corresponding parts must be equal. This is known as CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
$AB = EC$
[By CPCTC] ... (i)
$\angle BAD = \angle CED$
[By CPCTC] ... (ii)
It is also given that AD is the angle bisector of $\angle A$.
$\angle BAD = \angle CAD$
[Given] ... (iii)
From equations (ii) and (iii), we can equate the angles:
$\angle CAD = \angle CED$
Now, let's consider the triangle $\triangle ACE$.
In $\triangle ACE$, we have shown that $\angle CAE = \angle CEA$ (since $\angle CAD$ is the same as $\angle CAE$, and $\angle CED$ is the same as $\angle CEA$).
In a triangle, if two angles are equal, then the sides opposite to these equal angles are also equal.
The side opposite to $\angle CEA$ is AC.
The side opposite to $\angle CAE$ is EC.
Therefore, we can conclude that:
$AC = EC$
[Sides opposite to equal angles are equal] ... (iv)
From equation (i), we have $AB = EC$.
From equation (iv), we have $AC = EC$.
Comparing these two results, we get:
$AB = AC$
Since two sides of the triangle $\triangle ABC$ are equal, it is an isosceles triangle.
Hence, proved.
Sample Question 4: S is any point in the interior of ∆ PQR. Show that SQ + SR < PQ + PR.
Answer:
Given:
A triangle $\triangle PQR$.
S is any point in the interior of $\triangle PQR$.
To Prove:
$SQ + SR < PQ + PR$.
Construction Required:
Extend the line segment QS to intersect the side PR at a point T.
Proof:
We will use the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
First, consider the triangle $\triangle PQT$.
Applying the Triangle Inequality Theorem, we have:
$PQ + PT > QT$
From the figure, we can see that $QT = QS + ST$. Substituting this into the inequality:
$PQ + PT > QS + ST$
... (i)
Next, consider the triangle $\triangle STR$.
Applying the Triangle Inequality Theorem again, we get:
$ST + TR > SR$
... (ii)
Now, we add the two inequalities (i) and (ii):
$(PQ + PT) + (ST + TR) > (QS + ST) + SR$
Rearranging the terms on the left side:
$PQ + (PT + TR) + ST > QS + ST + SR$
From the figure, we can see that $PT + TR = PR$. Substituting this into the inequality:
$PQ + PR + ST > QS + SR + ST$
(Since T lies on PR)
Subtracting the common term $ST$ from both sides of the inequality, we are left with:
$PQ + PR > SQ + SR$
Or, written in the required format:
$SQ + SR < PQ + PR$
Hence, proved.
Exercise 7.4
Question 1. Find all the angles of an equilateral triangle.
Answer:
Solution:
An equilateral triangle is a triangle in which all three sides are equal in length.
Let's consider an equilateral triangle $\triangle ABC$.
By the definition of an equilateral triangle, we have:
$AB = BC = CA$
A fundamental property of triangles states that angles opposite to equal sides are also equal.
Since $BC = CA$, the angle opposite to side BC ($\angle A$) must be equal to the angle opposite to side CA ($\angle B$).
So, $\angle A = \angle B$.
Similarly, since $CA = AB$, the angle opposite to side CA ($\angle B$) must be equal to the angle opposite to side AB ($\angle C$).
So, $\angle B = \angle C$.
From these two relations, we can conclude that all three angles are equal:
$\angle A = \angle B = \angle C$
Let the measure of each of these equal angles be $x$.
According to the Angle Sum Property of a triangle, the sum of the measures of the interior angles of a triangle is always $180^\circ$.
Therefore, for $\triangle ABC$:
$\angle A + \angle B + \angle C = 180^\circ$
Substituting $x$ for each angle, we get:
$x + x + x = 180^\circ$
$3x = 180^\circ$
To find the value of $x$, we divide both sides by 3:
$x = \frac{180^\circ}{3}$
$x = 60^\circ$
Thus, all the angles of an equilateral triangle are equal, and each angle measures $60^\circ$.
$\angle A = 60^\circ, \angle B = 60^\circ, \text{ and } \angle C = 60^\circ$.
Question 2. The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in Fig. 7.12. Prove that the image is as far behind the mirror as the object is in front of the mirror.

[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
Answer:
Given:
In Fig. 7.12, LM is a plane mirror. An object is placed at point A, and its virtual image is formed at point B. A light ray from A, the incident ray AC, strikes the mirror at C and reflects as the reflected ray CD. An observer at D sees the image at B. CN is the normal to the mirror at point C.
According to the laws of reflection, the angle of incidence ($i$) is equal to the angle of reflection ($r$).
$\angle i = \angle r$
which means,
$\angle ACN = \angle DCN$
... (i)
To Prove:
The image is as far behind the mirror as the object is in front of the mirror. This means the perpendicular distance from A to the mirror LM is equal to the perpendicular distance from B to the mirror LM.
Proof:
Let's draw a line segment from A, perpendicular to the mirror LM, meeting it at a point P. The distance of the object from the mirror is AP. For a plane mirror, the image B lies on the line AP extended such that A, P, and B are collinear, and the line segment AB is perpendicular to the mirror LM.
Since the normal CN is also perpendicular to the mirror LM, the lines AB and CN are parallel to each other.
$AB \parallel CN$
(Both are perpendicular to the same line LM)
Now, consider AC as a transversal intersecting the parallel lines AB and CN. The alternate interior angles are equal.
$\angle BAC = \angle ACN$
(Alternate interior angles)
From equation (i), we know $\angle ACN = i$. Therefore,
$\angle BAC = i$
... (ii)
The reflected ray is CD. For a virtual image, this ray appears to come from the image point B. This means that the points B, C, and the direction of the reflected ray are on the same straight line. So, the line passing through B and C is the same as the line passing through C and D.
Consider the line BCD as a transversal intersecting the parallel lines AB and CN. The corresponding angles are equal.
$\angle ABC = \angle DCN$
(Corresponding angles)
From equation (i), we know $\angle DCN = r$. Therefore,
$\angle ABC = r$
... (iii)
From the law of reflection, we are given that $i = r$. Using the results from equations (ii) and (iii), we can conclude:
$\angle BAC = \angle ABC$
In $\triangle ABC$, since two angles are equal, the sides opposite to these angles must also be equal. Therefore, $\triangle ABC$ is an isosceles triangle.
AC = BC
(Sides opposite to equal angles)
Now, let's consider the two right-angled triangles, $\triangle APC$ and $\triangle BPC$.
$\angle APC = \angle BPC = 90^\circ$
(Since $AB \perp LM$)
AC = BC
(Proved above)
PC = PC
(Common side)
By the RHS (Right angle-Hypotenuse-Side) congruence criterion, the two triangles are congruent.
$\triangle APC \cong \triangle BPC$
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
$AP = BP$
This shows that the perpendicular distance of the object A from the mirror (AP) is equal to the perpendicular distance of the image B from the mirror (BP).
Hence, it is proved that the image is as far behind the mirror as the object is in front of the mirror.
Question 3. ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Fig. 7.13). To prove that ∠BAD = ∠CAD, a student proceeded as follows:

In ∆ ABD and ∆ ACD,
AB = AC (Given)
∠B = ∠C (because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ ABD ≅ ∆ ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
Answer:
The Defect in the Argument:
The student's argument contains a logical flaw known as circular reasoning. The defect lies in the second step of the proof:
$\angle B = \angle C$ (because AB = AC)
While it is true that in an isosceles triangle, angles opposite to equal sides are equal, the standard proof of this theorem itself relies on what the student is trying to prove. To prove that $\angle B = \angle C$ given $AB = AC$, one typically constructs the angle bisector of $\angle A$ and then proves the two smaller triangles are congruent. The student is trying to prove that the altitude AD is also the angle bisector, but they are using a property ($\angle B = \angle C$) which is a consequence of the angle bisector also being the altitude.
In essence, the student is assuming a result that is logically dependent on the conclusion they are trying to reach. A valid proof must be built only upon the initial given information and fundamental axioms, not on subsequent theorems that are derived from the conclusion itself.
The Correct Proof:
The correct way to prove that $\angle BAD = \angle CAD$ is by using the RHS (Right angle-Hypotenuse-Side) congruence criterion, which does not depend on the equality of $\angle B$ and $\angle C$.
Given:
An isosceles triangle $\triangle ABC$ with $AB = AC$.
$AD \perp BC$, which means $\angle ADB = \angle ADC = 90^\circ$.
To Prove:
$\angle BAD = \angle CAD$.
Proof:
Consider the two right-angled triangles, $\triangle ABD$ and $\triangle ACD$.
$\angle ADB = \angle ADC = 90^\circ$
(Given that $AD \perp BC$)
AB = AC
(Given, Hypotenuse of the triangles)
AD = AD
(Common side)
Thus, by the RHS congruence rule, the two triangles are congruent.
$\triangle ABD \cong \triangle ACD$
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, $\angle BAD = \angle CAD$.
This proof is valid because it only uses the given information and a fundamental congruence rule (RHS) without circular logic.
Question 4. P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
Answer:
Given:
1. A point P lies on the bisector of $\angle ABC$. Let the bisector be the ray BP.
This implies that $\angle ABP = \angle PBC$.
2. A line passing through P is parallel to the ray BA.
3. This parallel line intersects the ray BC at a point Q. Thus, $PQ \parallel BA$.
To Prove:
The triangle BPQ is an isosceles triangle.
Proof:
We are given that the ray BP is the bisector of $\angle ABC$.
By the definition of an angle bisector, the angle is divided into two equal parts.
$\angle ABP = \angle PBC$
(BP bisects $\angle ABC$)
Since the point Q lies on the ray BC, the angle $\angle PBC$ is the same as $\angle PBQ$.
$\angle ABP = \angle PBQ$
... (i)
We are also given that the line segment PQ is parallel to the ray BA ($PQ \parallel BA$).
Now, let's consider the line segment BP as a transversal that intersects the two parallel lines PQ and BA.
When a transversal intersects two parallel lines, the pair of alternate interior angles are equal.
In this case, $\angle BPQ$ and $\angle ABP$ are alternate interior angles.
$\angle BPQ = \angle ABP$
[Alternate interior angles] ... (ii)
Now, comparing equations (i) and (ii), we can see that both $\angle PBQ$ and $\angle BPQ$ are equal to $\angle ABP$.
Therefore, we can conclude that:
$\angle PBQ = \angle BPQ$
In $\triangle BPQ$, we have now shown that two of its angles are equal.
A fundamental property of triangles states that if two angles in a triangle are equal, then the sides opposite to these equal angles are also equal.
The side opposite to $\angle BPQ$ is BQ.
The side opposite to $\angle PBQ$ is PQ.
Therefore, we must have:
$PQ = BQ$
A triangle with two equal sides is defined as an isosceles triangle.
Hence, $\triangle BPQ$ is an isosceles triangle.
Hence, proved.
Question 5. ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
Answer:
Given:
A quadrilateral ABCD in which the adjacent sides are equal.
1. $AB = BC$
2. $AD = CD$
To Prove:
The diagonal BD bisects both $\angle ABC$ and $\angle ADC$.
This means we need to show:
1. $\angle ABD = \angle CBD$
2. $\angle ADB = \angle CDB$
Proof:
To prove that the diagonal BD bisects the angles, we will show that it divides the quadrilateral into two congruent triangles, namely $\triangle ABD$ and $\triangle CBD$.
In $\triangle ABD$ and $\triangle CBD$, we compare the corresponding sides:
AB = CB
(Given)
AD = CD
(Given)
BD = BD
(Common side to both triangles)
Since all three corresponding sides of the triangles are equal, the two triangles are congruent by the SSS (Side-Side-Side) congruence criterion.
Therefore, $\triangle ABD \cong \triangle CBD$.
Since the triangles are congruent, their corresponding parts must be equal. This property is known as CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
By CPCTC, the corresponding angles are equal:
$\angle ABD = \angle CBD$
(By CPCTC)
This equality shows that the line segment BD divides $\angle ABC$ into two equal angles. Therefore, BD bisects $\angle ABC$.
Similarly, by CPCTC:
$\angle ADB = \angle CDB$
(By CPCTC)
This equality shows that the line segment BD divides $\angle ADC$ into two equal angles. Therefore, BD bisects $\angle ADC$.
Thus, we have shown that the diagonal BD bisects both $\angle ABC$ and $\angle ADC$.
Hence, proved.
Question 6. ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2 AD.
Answer:
Given:
1. $\triangle ABC$ is a right-angled triangle.
2. It is also an isosceles triangle with $AB = AC$.
3. The ray AD is the bisector of $\angle A$ and meets the side BC at point D.
To Prove:
$BC = 2 AD$.
Proof:
In $\triangle ABC$, since it is an isosceles triangle with $AB = AC$, the angles opposite to these equal sides must also be equal.
Therefore, $\angle ABC = \angle ACB$.
Also, since $\triangle ABC$ is a right-angled triangle and the two legs AB and AC are equal, the right angle must be at vertex A (as the hypotenuse is the longest side). So, $\angle BAC = 90^\circ$.
Using the Angle Sum Property of a triangle:
$\angle BAC + \angle ABC + \angle ACB = 180^\circ$
$90^\circ + \angle ABC + \angle ABC = 180^\circ$ (Since $\angle ABC = \angle ACB$)
$2 \angle ABC = 180^\circ - 90^\circ$
$2 \angle ABC = 90^\circ$
$\angle ABC = \frac{90^\circ}{2} = 45^\circ$
Thus, $\angle ABC = \angle ACB = 45^\circ$.
Now, it is given that AD is the bisector of $\angle BAC$.
$\angle BAD = \angle CAD = \frac{\angle BAC}{2} = \frac{90^\circ}{2} = 45^\circ$.
Let's consider the triangle $\triangle ABD$.
We have $\angle ABD = 45^\circ$ (proved above) and $\angle BAD = 45^\circ$ (proved above).
Since two angles of $\triangle ABD$ are equal, it is an isosceles triangle. The sides opposite to these equal angles must be equal.
Side opposite to $\angle ABD$ is AD.
Side opposite to $\angle BAD$ is BD.
AD = BD
... (i)
Similarly, let's consider the triangle $\triangle ACD$.
We have $\angle ACD = 45^\circ$ (proved above) and $\angle CAD = 45^\circ$ (proved above).
Since two angles of $\triangle ACD$ are equal, it is also an isosceles triangle. The sides opposite to these equal angles must be equal.
Side opposite to $\angle ACD$ is AD.
Side opposite to $\angle CAD$ is CD.
AD = CD
... (ii)
The side BC is the sum of the lengths of the segments BD and CD.
$BC = BD + CD$
Substituting the values from equations (i) and (ii):
$BC = AD + AD$
$BC = 2 AD$
Hence, proved.
Alternate Solution (Using Congruence)
Consider $\triangle ABD$ and $\triangle ACD$.
AB = AC
(Given)
$\angle BAD = \angle CAD$
(AD is the angle bisector)
AD = AD
(Common side)
By SAS (Side-Angle-Side) congruence criterion, $\triangle ABD \cong \triangle ACD$.
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
$BD = CD$. This means D is the midpoint of BC, and AD is the median to the hypotenuse.
Also by CPCTC, $\angle ADB = \angle ADC$.
Since $\angle ADB$ and $\angle ADC$ form a linear pair, $\angle ADB + \angle ADC = 180^\circ$.
$2 \angle ADB = 180^\circ \implies \angle ADB = 90^\circ$.
So, AD is perpendicular to BC.
In the right-angled $\triangle ADB$, we have $\angle ABD = 45^\circ$ and $\angle ADB = 90^\circ$.
So, $\angle BAD = 180^\circ - 90^\circ - 45^\circ = 45^\circ$.
Since $\angle ABD = \angle BAD = 45^\circ$, $\triangle ADB$ is an isosceles triangle with $AD = BD$.
We know $BC = BD + CD$. Since $BD = CD$, we have $BC = 2 BD$.
Substituting $BD = AD$, we get:
$BC = 2 AD$
Hence, proved.
Question 7. O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆ OCD is an isosceles triangle.
Answer:
Given:
1. ABCD is a square. This means all its sides are equal and all its interior angles are $90^\circ$.
$AB = BC = CD = DA$
$\angle DAB = \angle ABC = \angle BCD = \angle CDA = 90^\circ$
2. O is a point in the interior of the square such that $\triangle OAB$ is an equilateral triangle.
This means all sides of $\triangle OAB$ are equal and all its angles are $60^\circ$.
$OA = OB = AB$
$\angle OAB = \angle OBA = \angle AOB = 60^\circ$
To Prove:
$\triangle OCD$ is an isosceles triangle. (This requires proving that two of its sides, OC and OD, are equal).
Proof:
From the properties of the square and the equilateral triangle, we can establish a relationship between their sides.
Since $AB = BC = CD = DA$ (sides of a square) and $OA = OB = AB$ (sides of an equilateral triangle), we can conclude that:
$OA = OB = AB = BC = CD = DA$.
Now, let's find the measure of the angles $\angle DAO$ and $\angle CBO$.
We know that $\angle DAB = 90^\circ$ (angle of a square) and $\angle OAB = 60^\circ$ (angle of an equilateral triangle).
$\angle DAO = \angle DAB - \angle OAB$
$\angle DAO = 90^\circ - 60^\circ = 30^\circ$
Similarly, we know that $\angle ABC = 90^\circ$ (angle of a square) and $\angle OBA = 60^\circ$ (angle of an equilateral triangle).
$\angle CBO = \angle ABC - \angle OBA$
$\angle CBO = 90^\circ - 60^\circ = 30^\circ$
So, we have $\angle DAO = \angle CBO = 30^\circ$.
Now, we will prove the congruence of $\triangle ODA$ and $\triangle OCB$ to show that $OD = OC$.
In $\triangle ODA$ and $\triangle OCB$:
DA = CB
(Sides of the square ABCD)
$\angle DAO = \angle CBO$
(Both are $30^\circ$, as proved above)
OA = OB
(Sides of the equilateral triangle OAB)
Therefore, by the SAS (Side-Angle-Side) congruence criterion, the two triangles are congruent.
$\triangle ODA \cong \triangle OCB$
Since the triangles are congruent, their corresponding parts are equal. This property is known as CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
The side corresponding to OD in $\triangle ODA$ is OC in $\triangle OCB$.
Therefore, $OD = OC$.
Now, in $\triangle OCD$, we have two sides, OD and OC, that are equal in length.
A triangle with two equal sides is an isosceles triangle.
Hence, $\triangle OCD$ is an isosceles triangle.
Hence, proved.
Question 8. ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
Answer:
Given:
Two triangles, $\triangle ABC$ and $\triangle DBC$, are on the same base BC.
Points A and D are on opposite sides of the line segment BC.
$\triangle ABC$ is an isosceles triangle with $AB = AC$.
$\triangle DBC$ is an isosceles triangle with $DB = DC$.
To Prove:
The line segment AD is the perpendicular bisector of the line segment BC.
This means we need to prove two things:
1. AD bisects BC (i.e., if AD intersects BC at E, then $BE = CE$).
2. AD is perpendicular to BC (i.e., $\angle AEB = 90^\circ$).
Proof:
Let the line segment AD intersect the base BC at a point E.
First, we will establish the congruence of $\triangle ABD$ and $\triangle ACD$.
In $\triangle ABD$ and $\triangle ACD$:
AB = AC
(Given)
DB = DC
(Given)
AD = AD
(Common side)
By the SSS (Side-Side-Side) congruence criterion, we have:
$\triangle ABD \cong \triangle ACD$
Since the triangles are congruent, their corresponding parts are equal (CPCTC - Corresponding Parts of Congruent Triangles are Congruent). Therefore:
$\angle BAE = \angle CAE$
... (i)
(This is because $\angle BAD$ and $\angle CAD$ are corresponding angles, and E lies on the line segment AD).
Now, let's consider the triangles $\triangle ABE$ and $\triangle ACE$.
In $\triangle ABE$ and $\triangle ACE$:
AB = AC
(Given)
$\angle BAE = \angle CAE$
(From equation (i))
AE = AE
(Common side)
By the SAS (Side-Angle-Side) congruence criterion, we have:
$\triangle ABE \cong \triangle ACE$
By CPCTC, the corresponding parts of these triangles are equal. Therefore:
1. $BE = CE$
This proves that the line AD bisects the side BC at point E.
2. $\angle AEB = \angle AEC$
We know that BC is a straight line, so the angles $\angle AEB$ and $\angle AEC$ form a linear pair.
$\angle AEB + \angle AEC = 180^\circ$
Substituting $\angle AEC$ with $\angle AEB$ (since they are equal):
$\angle AEB + \angle AEB = 180^\circ$
$2\angle AEB = 180^\circ$
$\angle AEB = \frac{180^\circ}{2} = 90^\circ$
This proves that the line AD is perpendicular to the side BC.
Since AD bisects BC and is also perpendicular to BC, we can conclude that AD is the perpendicular bisector of BC.
Hence, proved.
Question 9. ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.
Answer:
Given:
1. $\triangle ABC$ is an isosceles triangle with $AC = BC$.
2. AD and BE are altitudes to the sides BC and AC respectively. This means:
$AD \perp BC \implies \angle ADB = 90^\circ$
$BE \perp AC \implies \angle BEA = 90^\circ$
To Prove:
$AE = BD$.
Proof:
Since $\triangle ABC$ is an isosceles triangle with $AC = BC$, the angles opposite to these equal sides must also be equal.
$\angle CAB = \angle CBA$
(Angles opposite to equal sides are equal)
These angles can also be written as $\angle EAB = \angle DBA$.
Now, let's consider the triangles $\triangle ABE$ and $\triangle BAD$.
In $\triangle ABE$ and $\triangle BAD$:
$\angle BEA = \angle ADB$
(Each is $90^\circ$, as BE and AD are altitudes)
$\angle EAB = \angle DBA$
(Proved above)
AB = BA
(Common side)
Therefore, by the AAS (Angle-Angle-Side) congruence criterion, the two triangles are congruent.
$\triangle ABE \cong \triangle BAD$
Since the triangles are congruent, their corresponding parts must be equal (by CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
The side AE in $\triangle ABE$ corresponds to the side BD in $\triangle BAD$.
Hence, $AE = BD$.
Hence, proved.
Alternate Solution:
Let's consider the triangles $\triangle ADC$ and $\triangle BEC$.
$\angle ADC = \angle BEC$
(Each is $90^\circ$, as AD and BE are altitudes)
$\angle C = \angle C$
(Common angle)
AC = BC
(Given)
By the AAS (Angle-Angle-Side) congruence criterion, we have:
$\triangle ADC \cong \triangle BEC$
By CPCTC, their corresponding parts are equal. Therefore:
DC = EC
[By CPCTC] ... (i)
We are given that the entire sides are equal:
AC = BC
[Given] ... (ii)
The side AC can be written as the sum of its parts, $AE + EC$.
The side BC can be written as the sum of its parts, $BD + DC$.
Substituting these into equation (ii):
$AE + EC = BD + DC$
From equation (i), we know that $EC = DC$. We can substitute this into the above equation:
$AE + EC = BD + EC$
Subtracting the common term $EC$ from both sides, we get:
$AE = BD$
Hence, proved.
Question 10. Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Answer:
Given:
A triangle $\triangle ABC$ in which AD is the median to the side BC. This means D is the midpoint of BC, so $BD = DC$.
To Prove:
The sum of the two sides AB and AC is greater than twice the median AD.
$AB + AC > 2 AD$.
Construction Required:
Produce the median AD to a point E such that $AD = DE$. Join the point E to C.
Proof:
We will first establish the congruence between $\triangle ADB$ and $\triangle EDC$.
In $\triangle ADB$ and $\triangle EDC$:
AD = ED
(By Construction)
$\angle ADB = \angle EDC$
(Vertically opposite angles)
BD = CD
(Given that AD is the median)
Therefore, by the SAS (Side-Angle-Side) congruence criterion, the two triangles are congruent.
$\triangle ADB \cong \triangle EDC$
Since the triangles are congruent, their corresponding parts must be equal (by CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
The side AB in $\triangle ADB$ corresponds to the side EC in $\triangle EDC$.
$AB = EC$
[By CPCTC] ... (i)
Now, let's consider the newly formed triangle $\triangle ACE$.
According to the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
Applying this theorem to $\triangle ACE$, we get:
$AC + EC > AE$
(Triangle Inequality Theorem)
From our construction, we know that the length of the side AE is the sum of AD and DE.
$AE = AD + DE$
Since $AD = DE$ by construction, we have:
$AE = AD + AD = 2 AD$
Now, we substitute $EC = AB$ (from equation (i)) and $AE = 2 AD$ into the triangle inequality:
$AC + AB > 2 AD$
This can be rewritten as:
$AB + AC > 2 AD$
Hence, it is proved that the sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Question 11. Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2 (BD + AC)
Answer:
Given:
A quadrilateral ABCD with diagonals AC and BD.
To Prove:
$AB + BC + CD + DA < 2 (BD + AC)$.
Proof:
Let the diagonals AC and BD of the quadrilateral ABCD intersect at a point O.
We will use the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
We apply this theorem to the four triangles formed by the intersection of the diagonals:
1. In $\triangle OAB$:
$OA + OB > AB$
... (i)
2. In $\triangle OBC$:
$OB + OC > BC$
... (ii)
3. In $\triangle OCD$:
$OC + OD > CD$
... (iii)
4. In $\triangle ODA$:
$OD + OA > DA$
... (iv)
Now, we add the four inequalities (i), (ii), (iii), and (iv):
$(OA + OB) + (OB + OC) + (OC + OD) + (OD + OA) > AB + BC + CD + DA$
By rearranging and grouping the terms on the left-hand side, we get:
$(OA + OA) + (OB + OB) + (OC + OC) + (OD + OD) > AB + BC + CD + DA$
$2 OA + 2 OB + 2 OC + 2 OD > AB + BC + CD + DA$
Let's group the parts of the diagonals together:
$(2 OA + 2 OC) + (2 OB + 2 OD) > AB + BC + CD + DA$
$2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA$
From the figure, we can see that the sum of the parts of the diagonals equals the total length of the diagonals:
$OA + OC = AC$
$OB + OD = BD$
Substituting these back into our inequality:
$2(AC) + 2(BD) > AB + BC + CD + DA$
$2(AC + BD) > AB + BC + CD + DA$
Flipping the inequality to match the required format, we have:
$AB + BC + CD + DA < 2 (BD + AC)$
Hence, proved.
Question 12. Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD.
Answer:
Given:
A quadrilateral ABCD with diagonals AC and BD.
To Prove:
The sum of the lengths of the sides of the quadrilateral is greater than the sum of the lengths of its diagonals.
$AB + BC + CD + DA > AC + BD$.
Proof:
The proof relies on the repeated application of the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
We can view the quadrilateral as being composed of several triangles.
1. Consider the triangle $\triangle ABC$:
Applying the Triangle Inequality Theorem, the sum of sides AB and BC is greater than the side AC.
$AB + BC > AC$
... (i)
2. Consider the triangle $\triangle ADC$:
Applying the Triangle Inequality Theorem, the sum of sides AD and CD is greater than the side AC.
$AD + CD > AC$
... (ii)
3. Consider the triangle $\triangle ABD$:
Applying the Triangle Inequality Theorem, the sum of sides AB and AD is greater than the side BD.
$AB + AD > BD$
... (iii)
4. Consider the triangle $\triangle BCD$:
Applying the Triangle Inequality Theorem, the sum of sides BC and CD is greater than the side BD.
$BC + CD > BD$
... (iv)
Now, we add the four inequalities (i), (ii), (iii), and (iv):
$(AB + BC) + (AD + CD) + (AB + AD) + (BC + CD) > AC + AC + BD + BD$
By grouping the like terms on the left-hand side, we get:
$(AB + AB) + (BC + BC) + (CD + CD) + (AD + AD) > 2 AC + 2 BD$
$2 AB + 2 BC + 2 CD + 2 AD > 2 AC + 2 BD$
Factoring out the common factor of 2 from both sides:
$2 (AB + BC + CD + AD) > 2 (AC + BD)$
Dividing both sides of the inequality by 2, we get the final result:
$AB + BC + CD + DA > AC + BD$
Hence, proved.
Question 13. In a triangle ABC, D is the mid-point of side AC such that BD = $\frac{1}{2}$ AC. Show that ∠ABC is a right angle.
Answer:
Given:
In a triangle $\triangle ABC$, D is the mid-point of side AC.
This implies $AD = DC$.
It is also given that $BD = \frac{1}{2} AC$.
To Prove:
$\angle ABC$ is a right angle, i.e., $\angle ABC = 90^\circ$.
Proof:
Since D is the mid-point of the side AC, the length of AC can be expressed as:
$AC = AD + DC$
Given that $AD = DC$, we can write $AC = AD + AD = 2 AD$.
From this, it follows that $AD = \frac{1}{2} AC$.
We are also given that $BD = \frac{1}{2} AC$.
Comparing these two results, we find that:
$BD = AD$.
Since we already know $AD = DC$, we can conclude that all three segments are equal:
AD = BD = DC
... (i)
Now, let's analyze the two smaller triangles formed by the median BD.
In triangle $\triangle ADB$:
Since $AD = BD$, $\triangle ADB$ is an isosceles triangle. In an isosceles triangle, the angles opposite to the equal sides are also equal.
Therefore, $\angle BAD = \angle ABD$. Let's denote this angle as $x$.
$\angle BAD = \angle ABD = x$
... (ii)
In triangle $\triangle CDB$:
Since $DC = BD$, $\triangle CDB$ is also an isosceles triangle.
Therefore, $\angle BCD = \angle CBD$. Let's denote this angle as $y$.
$\angle BCD = \angle CBD = y$
... (iii)
Now, consider the entire triangle $\triangle ABC$. According to the Angle Sum Property of a triangle, the sum of its interior angles is $180^\circ$.
$\angle CAB + \angle ABC + \angle BCA = 180^\circ$
We can express these angles in terms of $x$ and $y$:
$\angle CAB = \angle BAD = x$
$\angle BCA = \angle BCD = y$
$\angle ABC = \angle ABD + \angle CBD = x + y$
Substituting these into the angle sum equation:
$x + (x + y) + y = 180^\circ$
$2x + 2y = 180^\circ$
$2(x + y) = 180^\circ$
$x + y = \frac{180^\circ}{2}$
$x + y = 90^\circ$
Since we defined $\angle ABC = x + y$, we have:
$\angle ABC = 90^\circ$
Hence, proved.
Alternate Solution (Using Converse of a Theorem):
This problem is the converse of the theorem which states: "The median to the hypotenuse of a right-angled triangle is half the length of the hypotenuse."
We are given that D is the mid-point of AC, which means $AD = DC = \frac{1}{2} AC$.
We are also given that $BD = \frac{1}{2} AC$.
From this, we can conclude that $AD = DC = BD$.
This result shows that the point D is equidistant from the three vertices A, B, and C of the triangle.
Therefore, if we consider D as the center, we can draw a circle with radius $r = AD = BD = DC$ that passes through all three vertices A, B, and C.
In this circle, the line segment AC is a chord that passes through the center D. Hence, AC is the diameter of the circle.
According to a fundamental theorem of circles, the angle in a semicircle is a right angle. This means the angle subtended by a diameter at any point on the circumference is $90^\circ$.
Here, AC is the diameter and B is a point on the circumference. The angle subtended by AC at B is $\angle ABC$.
Therefore, $\angle ABC = 90^\circ$.
Hence, proved.
Question 14. In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.
Answer:
Given:
A right-angled triangle $\triangle ABC$, with the right angle at vertex B ($\angle ABC = 90^\circ$).
D is the mid-point of the hypotenuse AC. This means $AD = DC = \frac{1}{2} AC$.
To Prove:
The line segment joining the mid-point D to the opposite vertex B is half the length of the hypotenuse AC.
We need to prove that $BD = \frac{1}{2} AC$.
Construction Required:
Draw a line through the point D parallel to the side BC, and let it intersect the side AB at a point E.
Proof:
In the larger triangle $\triangle ABC$:
We are given that D is the mid-point of the side AC.
By our construction, the line segment DE is parallel to the side BC ($DE \parallel BC$).
According to the Converse of the Mid-point Theorem, a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Therefore, the point E must be the mid-point of the side AB.
$AE = EB$
... (i)
Also, since $DE \parallel BC$ and AB is a transversal line, the corresponding angles are equal.
$\angle AED = \angle ABC$
Since we are given that $\angle ABC = 90^\circ$, it follows that $\angle AED = 90^\circ$.
Now, consider the two triangles $\triangle ADE$ and $\triangle BDE$.
$AE = EB$
(From equation (i))
$\angle AED = \angle BED$
(Both are $90^\circ$, as they form a linear pair)
DE = DE
(Common side)
By the SAS (Side-Angle-Side) congruence criterion, the two triangles are congruent.
$\triangle ADE \cong \triangle BDE$
Since the triangles are congruent, their corresponding parts must be equal (by CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
The side AD in $\triangle ADE$ corresponds to the side BD in $\triangle BDE$.
Therefore, $AD = BD$.
We were initially given that D is the mid-point of the hypotenuse AC, which means:
$AD = \frac{1}{2} AC$
By equating the two expressions for AD, we get:
$BD = \frac{1}{2} AC$
Hence, proved.
Alternate Solution:
Construction: Produce the line segment BD to a point E such that $BD = DE$. Join E to C.
Proof:
Consider the triangles $\triangle ADB$ and $\triangle CDE$.
$AD = CD$
(Given, D is the midpoint of AC)
$\angle ADB = \angle CDE$
(Vertically opposite angles)
BD = DE
(By construction)
By SAS congruence, $\triangle ADB \cong \triangle CDE$.
By CPCTC, we have $AB = CE$ and $\angle ABD = \angle CED$.
Since $\angle ABD$ and $\angle CED$ are alternate interior angles for lines AB and CE with transversal BE, their equality implies that $AB \parallel CE$.
Now, we have a pair of opposite sides, AB and CE, that are both equal and parallel. This is a property of a parallelogram. Thus, ABCE is a parallelogram.
In a parallelogram, consecutive angles are supplementary. So, $\angle ABC + \angle BCE = 180^\circ$.
Since $\angle ABC = 90^\circ$ (given), we have $90^\circ + \angle BCE = 180^\circ$, which means $\angle BCE = 90^\circ$.
A parallelogram with one right angle is a rectangle. Therefore, ABCE is a rectangle.
A property of rectangles is that their diagonals are equal in length and bisect each other.
The diagonals of rectangle ABCE are AC and BE.
Therefore, $AC = BE$.
From our construction, we have $BE = BD + DE$. Since $BD = DE$, we can write $BE = 2 BD$.
Substituting this into the diagonal equality:
$AC = 2 BD$
Rearranging this gives:
$BD = \frac{1}{2} AC$
Hence, proved.
Question 15. Two lines l and m intersect at the point O and P is a point on a line n passing through the point O such that P is equidistant from l and m. Prove that n is the bisector of the angle formed by l and m.
Answer:
Given:
1. Two lines, l and m, intersect at a point O.
2. A third line, n, passes through the point O.
3. P is a point on line n.
4. The point P is equidistant from lines l and m. This means the perpendicular distance from P to line l is equal to the perpendicular distance from P to line m.
To Prove:
The line n is the bisector of the angle formed by the lines l and m.
Proof:
Let's draw perpendiculars from the point P to the lines l and m.
Let PQ be the perpendicular from P to line l, so $PQ \perp l$.
Let PR be the perpendicular from P to line m, so $PR \perp m$.
By definition, the distance from P to line l is the length of the segment PQ, and the distance from P to line m is the length of the segment PR.
Since P is given to be equidistant from l and m, we have:
PQ = PR
(Given)
Now, consider the two right-angled triangles, $\triangle OPQ$ and $\triangle OPR$.
In $\triangle OPQ$ and $\triangle OPR$:
$\angle OQP = \angle ORP$
(Each is $90^\circ$, by construction of perpendiculars)
OP = OP
(Common hypotenuse to both triangles)
PQ = PR
(Given that P is equidistant)
Therefore, by the RHS (Right angle-Hypotenuse-Side) congruence criterion, the two triangles are congruent.
$\triangle OPQ \cong \triangle OPR$
Since the triangles are congruent, their corresponding parts must be equal. This property is known as CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
The angle $\angle POQ$ in $\triangle OPQ$ corresponds to the angle $\angle POR$ in $\triangle OPR$.
Hence, $\angle POQ = \angle POR$.
This shows that the line segment OP (which is part of the line n) divides the angle formed by lines l and m into two equal angles.
Therefore, the line n is the bisector of the angle formed by l and m.
Hence, proved.
Question 16. Line segment joining the mid-points M and N of parallel sides AB and DC, respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD = BC.
Answer:
Given:
1. A trapezium ABCD with parallel sides $AB \parallel DC$.
2. M is the mid-point of side AB, which means $AM = MB$.
3. N is the mid-point of side DC, which means $DN = NC$.
4. The line segment MN is perpendicular to both AB and DC.
This implies $\angle AMN = 90^\circ$ and $\angle DNM = 90^\circ$.
To Prove:
The non-parallel sides are equal, i.e., $AD = BC$.
Proof:
First, we will prove that the triangles formed by the line segment MN and the non-parallel sides are congruent.
Consider the triangles $\triangle DNM$ and $\triangle CNM$.
DN = CN
(Given, N is the mid-point of DC)
$\angle DNM = \angle CNM = 90^\circ$
(Given, $MN \perp DC$)
MN = MN
(Common side)
Therefore, by the SAS (Side-Angle-Side) congruence criterion, the two triangles are congruent.
$\triangle DNM \cong \triangle CNM$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), their corresponding parts are equal.
$DM = CM$
[By CPCTC] ... (i)
$\angle DMN = \angle CMN$
[By CPCTC] ... (ii)
Now, let's consider the triangles $\triangle ADM$ and $\triangle BCM$.
We need to compare their sides and included angles.
AM = BM
(Given, M is the mid-point of AB)
DM = CM
(From equation (i))
For the included angle, we are given that $MN \perp AB$, which means $\angle AMN = \angle BMN = 90^\circ$.
We can write the angle $\angle AMD$ as the sum of $\angle AMN$ and $\angle DMN$.
$\angle AMD = \angle AMN + \angle DMN = 90^\circ + \angle DMN$.
Similarly, we can write the angle $\angle BMC$ as the sum of $\angle BMN$ and $\angle CMN$.
$\angle BMC = \angle BMN + \angle CMN = 90^\circ + \angle CMN$.
From equation (ii), we know that $\angle DMN = \angle CMN$. Therefore, we can conclude that:
$\angle AMD = \angle BMC$
Now we have established the conditions for SAS congruence in $\triangle ADM$ and $\triangle BCM$.
By the SAS congruence criterion:
$\triangle ADM \cong \triangle BCM$
By CPCTC, the corresponding third sides of these congruent triangles must be equal.
$AD = BC$
Hence, proved.
Alternate Solution (Using Construction)
Construction Required: Draw a line through D parallel to MN, intersecting AB at P. Draw a line through C parallel to MN, intersecting AB at Q.
Proof:
Since $DP \parallel MN$ and $MN \perp AB$, it implies $DP \perp AB$. Similarly, $CQ \perp AB$.
Also, since $MN \perp DC$ and we have drawn $DP \parallel MN$ and $CQ \parallel MN$, the quadrilaterals DPNM and CQNM are rectangles.
In rectangle DPNM, opposite sides are equal, so $DN = PM$.
In rectangle CQNM, opposite sides are equal, so $CN = QM$.
We are given that N is the midpoint of DC, so $DN = CN$. Therefore, $PM = QM$.
Now, we are given that M is the midpoint of AB, so $AM = BM$.
Let's find the lengths of AP and BQ.
$AP = AM - PM$
$BQ = BM - QM$
Since $AM = BM$ and $PM = QM$, we can conclude that $AP = BQ$.
Now, consider the right-angled triangles $\triangle DPA$ and $\triangle CQB$.
$AP = BQ$
(Proved above)
$\angle DPA = \angle CQB = 90^\circ$
(By construction)
DP = CQ
(Both are equal to MN, the distance between parallel lines AB and DC)
By the SAS congruence criterion, $\triangle DPA \cong \triangle CQB$.
By CPCTC, their corresponding hypotenuses are equal.
$AD = BC$
Hence, proved.
Question 17. ABCD is a quadrilateral such that diagonal AC bisects the angles A and C. Prove that AB = AD and CB = CD.
Answer:
Given:
A quadrilateral ABCD in which the diagonal AC bisects both $\angle A$ and $\angle C$.
This means:
1. $\angle BAC = \angle DAC$
2. $\angle BCA = \angle DCA$
To Prove:
1. $AB = AD$
2. $CB = CD$
Proof:
The diagonal AC divides the quadrilateral ABCD into two triangles, namely $\triangle ABC$ and $\triangle ADC$.
To prove that the sides are equal, we will show that these two triangles are congruent.
In $\triangle ABC$ and $\triangle ADC$:
$\angle BAC = \angle DAC$
(Given, as AC bisects $\angle A$)
AC = AC
(Common side to both triangles)
$\angle BCA = \angle DCA$
(Given, as AC bisects $\angle C$)
Therefore, by the ASA (Angle-Side-Angle) congruence criterion, the two triangles are congruent.
$\triangle ABC \cong \triangle ADC$
Since the triangles are congruent, their corresponding parts must be equal. This property is known as CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
The side AB in $\triangle ABC$ corresponds to the side AD in $\triangle ADC$.
Hence, $AB = AD$.
Similarly, the side CB in $\triangle ABC$ corresponds to the side CD in $\triangle ADC$.
Hence, $CB = CD$.
Thus, both pairs of adjacent sides are proved to be equal.
Hence, proved.
Question 18. ABC is a right triangle such that AB = AC and bisector of angle C intersects the side AB at D. Prove that AC + AD = BC.
Answer:
Given:
1. ABC is a right-angled triangle. Since it is also an isosceles triangle with $AB = AC$, the right angle must be at vertex A. So, $\angle BAC = 90^\circ$.
2. The bisector of angle C, which is CD, intersects the side AB at point D. This means $\angle ACD = \angle BCD$.
To Prove:
$AC + AD = BC$.
Construction Required:
From the point D, draw a line segment perpendicular to the hypotenuse BC, meeting it at a point E. So, $DE \perp BC$.
Proof:
First, we determine the measures of the angles in $\triangle ABC$.
Since $AB = AC$, the angles opposite to these equal sides are also equal. Thus, $\angle ABC = \angle ACB$.
Using the Angle Sum Property in $\triangle ABC$:
$\angle BAC + \angle ABC + \angle ACB = 180^\circ$
$90^\circ + \angle ACB + \angle ACB = 180^\circ$
$2 \angle ACB = 90^\circ$
$\angle ACB = 45^\circ$.
Therefore, $\angle ABC = \angle ACB = 45^\circ$.
Since CD is the bisector of $\angle ACB$, it divides the angle into two equal parts:
$\angle ACD = \angle BCD = \frac{45^\circ}{2} = 22.5^\circ$.
Now, let's compare the two triangles $\triangle DAC$ and $\triangle DEC$.
$\angle DAC = 90^\circ$
(Given)
$\angle DEC = 90^\circ$
(By Construction)
So, $\angle DAC = \angle DEC$.
$\angle ACD = \angle ECD$
(As CD is the angle bisector)
CD = CD
(Common side)
By the AAS (Angle-Angle-Side) congruence criterion, the two triangles are congruent.
$\triangle DAC \cong \triangle DEC$
From the congruence, by CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
$AC = EC$
[By CPCTC] ... (i)
$AD = ED$
[By CPCTC] ... (ii)
Next, let's analyze the right-angled triangle $\triangle BDE$.
We know that $\angle DBE = \angle ABC = 45^\circ$.
We also know that $\angle BED = 90^\circ$ (by construction).
Using the Angle Sum Property in $\triangle BDE$:
$\angle BDE = 180^\circ - (\angle BED + \angle DBE) = 180^\circ - (90^\circ + 45^\circ) = 45^\circ$.
Since two angles of $\triangle BDE$ are equal ($\angle DBE = \angle BDE = 45^\circ$), it is an isosceles triangle.
Therefore, the sides opposite to these equal angles are also equal: $BE = ED$.
From equation (ii), we have $AD = ED$. Combining these two results, we get:
$AD = BE$
... (iii)
Now, we can write the full length of the hypotenuse BC as the sum of its segments:
$BC = BE + EC$
Substituting the results from equations (iii) for BE and (i) for EC:
$BC = AD + AC$
This can be rewritten as:
$AC + AD = BC$
Hence, proved.
Alternate Solution:
Construction Required:
Produce the line segment CA to a point E such that A lies between C and E, and the length of $AE$ is equal to the length of $AD$. Join the points D and E.
Proof:
Consider the triangle $\triangle ADE$.
By construction, we have $AE = AD$.
The angle $\angle DAE$ is formed by the line segment AD (which is on AB) and the line segment AE (on the line extending from AC). Since $AB \perp AC$, the angle $\angle DAE = 90^\circ$.
Therefore, $\triangle ADE$ is an isosceles right-angled triangle.
The base angles of an isosceles right triangle are each $45^\circ$. Thus,
$\angle ADE = \angle AED = 45^\circ$.
Now, let's consider the larger triangle $\triangle BCE$. We want to show that it is an isosceles triangle.
The angle $\angle CBE$ is the same as $\angle ABC$. As we found earlier, $\angle ABC = 45^\circ$. So, $\angle CBE = 45^\circ$.
The angle $\angle CEB$ is the same as $\angle AED$, which we just proved to be $45^\circ$. So, $\angle CEB = 45^\circ$.
Since two angles of $\triangle BCE$ are equal ($\angle CBE = \angle CEB = 45^\circ$), $\triangle BCE$ is an isosceles triangle.
In an isosceles triangle, the sides opposite the equal angles are equal in length.
$BC = CE$
From our construction, the length of the side CE is the sum of the lengths of CA and AE.
$CE = CA + AE$
By construction, we set $AE = AD$. Substituting this into the equation gives:
$CE = CA + AD$
Since we have already shown that $BC = CE$, we can conclude:
$AC + AD = BC$
Hence, proved.
Question 19. AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
Answer:
Given:
A quadrilateral ABCD where:
1. AB is the smallest side.
2. CD is the largest side.
To Find:
To determine which of the two angles, $\angle B$ or $\angle D$, is greater.
Construction Required:
Join the vertices B and D to form the diagonal BD. This divides the quadrilateral into two triangles, $\triangle ABD$ and $\triangle BCD$.
Solution:
The solution is based on the theorem: In a triangle, the angle opposite to the longer side is greater.
Step 1: Analyze $\triangle ABD$
We are given that AB is the smallest side of the quadrilateral. Therefore, the side AB must be shorter than the side AD.
$AB < AD$
In $\triangle ABD$, the angle opposite to side AB is $\angle ADB$, and the angle opposite to side AD is $\angle ABD$.
Applying the theorem, we get:
$\angle ADB < \angle ABD$
... (i)
Step 2: Analyze $\triangle BCD$
We are given that CD is the largest side of the quadrilateral. Therefore, the side CD must be longer than the side BC.
$BC < CD$
In $\triangle BCD$, the angle opposite to side BC is $\angle BDC$, and the angle opposite to side CD is $\angle CBD$.
Applying the theorem, we get:
$\angle BDC < \angle CBD$
... (ii)
Step 3: Combine the results
Now, we add the two inequalities (i) and (ii):
$(\angle ADB) + (\angle BDC) < (\angle ABD) + (\angle CBD)$
From the figure, we can combine the angles:
$\angle ADB + \angle BDC = \angle ADC$, which is the complete angle $\angle D$.
$\angle ABD + \angle CBD = \angle ABC$, which is the complete angle $\angle B$.
Substituting these back into our combined inequality, we get:
$\angle D < \angle B$
Therefore, we can conclude that $\angle B$ is greater than $\angle D$.
Question 20. Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than $\frac{2}{3}$ of a right angle.
Answer:
Given:
A triangle, which is not an equilateral triangle.
To Prove:
The angle opposite the longest side is greater than $\frac{2}{3}$ of a right angle.
Proof:
First, let's calculate the value of $\frac{2}{3}$ of a right angle.
A right angle is equal to $90^\circ$.
So, $\frac{2}{3}$ of a right angle = $\frac{2}{3} \times 90^\circ = 2 \times 30^\circ = 60^\circ$.
Therefore, we need to prove that the angle opposite the longest side is greater than $60^\circ$.
Let us consider a $\triangle ABC$ which is not equilateral. Let the sides opposite to angles $\angle A, \angle B, \angle C$ be $a, b, c$ respectively.
Without loss of generality, let's assume that side 'a' is the longest side of the triangle. This means:
$a \ge b$ and $a \ge c$.
Since the triangle is not equilateral, we cannot have $a = b = c$. So, at least one of the inequalities must be strict (i.e., $a > b$ or $a > c$).
We know that in a triangle, the angle opposite the longer side is greater. Thus, $\angle A$ is the largest angle in the triangle.
$\angle A \ge \angle B$ and $\angle A \ge \angle C$.
We also know that the sum of angles in any triangle is $180^\circ$.
$\angle A + \angle B + \angle C = 180^\circ$
... (i)
Now, let's use the method of contradiction. Let us assume that the angle opposite the longest side is not greater than $60^\circ$.
Our assumption is:
$\angle A \le 60^\circ$
... (ii)
Since $\angle A$ is the largest angle, it follows that:
$\angle B \le \angle A \implies \angle B \le 60^\circ$
$\angle C \le \angle A \implies \angle C \le 60^\circ$
Now, let's add these three inequalities:
$\angle A + \angle B + \angle C \le 60^\circ + 60^\circ + 60^\circ$
$\angle A + \angle B + \angle C \le 180^\circ$
However, from equation (i), we know that the sum of the angles must be exactly $180^\circ$.
The only way for the sum to be exactly $180^\circ$ under the conditions $\angle A \le 60^\circ, \angle B \le 60^\circ,$ and $\angle C \le 60^\circ$ is if all three angles are exactly $60^\circ$.
$\angle A = \angle B = \angle C = 60^\circ$
If all three angles of a triangle are $60^\circ$, then the triangle must be an equilateral triangle.
This contradicts the given information that the triangle is not an equilateral triangle.
Therefore, our initial assumption in (ii) must be false.
So, the angle opposite the longest side must be greater than $60^\circ$.
$\angle A > 60^\circ$
Hence, in a triangle, other than an equilateral triangle, the angle opposite the longest side is greater than $\frac{2}{3}$ of a right angle.
Hence Proved.
Question 21. ABCD is quadrilateral such that AB = AD and CB = CD. Prove that AC is the perpendicular bisector of BD.
Answer:
Given:
A quadrilateral ABCD in which AB = AD and CB = CD.
To Prove:
AC is the perpendicular bisector of BD.
This means we need to prove two things:
1. AC $\perp$ BD (i.e., the angle at their intersection is $90^\circ$).
2. AC bisects BD (i.e., BO = DO, where O is the intersection point).
Proof:
Let the diagonals AC and BD intersect at point O.
First, we consider $\triangle ABC$ and $\triangle ADC$.
AB = AD
(Given)
CB = CD
(Given)
AC = AC
(Common side)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle ABC \cong \triangle ADC$
By CPCTC (Corresponding parts of congruent triangles are equal), we have:
$\angle BAC = \angle DAC$
... (i)
This can also be written as $\angle BAO = \angle DAO$.
Now, we consider $\triangle ABO$ and $\triangle ADO$.
AB = AD
(Given)
$\angle BAO = \angle DAO$
[From (i)]
AO = AO
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle ABO \cong \triangle ADO$
By CPCTC, we have:
BO = DO
... (ii)
This shows that AC bisects BD.
Also by CPCTC,
$\angle AOB = \angle AOD$
... (iii)
Since BD is a straight line, the angles $\angle AOB$ and $\angle AOD$ form a linear pair.
$\angle AOB + \angle AOD = 180^\circ$
[Linear Pair Axiom]
Substituting $\angle AOD$ from (iii):
$\angle AOB + \angle AOB = 180^\circ$
$2\angle AOB = 180^\circ$
$\angle AOB = \frac{180^\circ}{2} = 90^\circ$
This shows that AC is perpendicular to BD.
From (ii), we have BO = DO, and we have just proved that $\angle AOB = 90^\circ$.
Therefore, AC is the perpendicular bisector of BD.
Hence Proved.
Alternate Solution:
We know that any point equidistant from the endpoints of a line segment lies on its perpendicular bisector.
In $\triangle ABD$, we are given:
AB = AD
This means point A is equidistant from points B and D. Therefore, A lies on the perpendicular bisector of the line segment BD.
Similarly, in $\triangle CBD$, we are given:
CB = CD
This means point C is equidistant from points B and D. Therefore, C also lies on the perpendicular bisector of the line segment BD.
Since both points A and C lie on the perpendicular bisector of BD, the line passing through A and C, which is the line AC, must be the perpendicular bisector of BD.
Hence Proved.

